
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Раздел 2. Технические и программные средства реализации информационных процессов ⇐ ПредыдущаяСтр 2 из 2
Вариант № 1 1. Перечислите элементы управления окном приложения 2. Операционная система (ОС) и ее состав. 3. Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант № 2 1. Состав персонального компьютера и назначение его основных функциональныхэлементов. 2. Назовите основные объекты ОС Windows Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №3 1. Классификация программного обеспечения. Виды программного обеспечения. 2. Назначение меню пользователя, системного меню и главного меню. Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №4 1. Операционные системы, состав, основные свойства и характеристики. 2. Назовите последовательность операций для создания папок, копирования и перемещения файлов. 3. Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №5 1. Запоминающие устройства: классификация, принцип работы, основные характеристики. 2. Основные служебные программы и их назначение. 3. Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №6 1. Виды и характеристики архиваторов. 2. Назовите основные принципы управления окном приложения. 3. Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант № 7 1. Состав и функции электронных таблиц Excel. Относительные и абсолютные ссылки  2. Перечислите элементы управления окном приложения 3.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант № 8 1. Состав персонального компьютера и назначение его основных функциональныхэлементов. 2. Назовите основные объекты ОС Windows 3.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №9 1. Классификация программного обеспечения. Виды программного обеспечения. 2. Назначение меню пользователя, системного меню и главного меню. 3.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №10 1. Операционные системы, состав, основные свойства и характеристики. 2. Назовите последовательность операций для создания папок, копирования и перемещения файлов. 3.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №11
1. Запоминающие устройства: классификация, принцип работы, основные характеристики. 2. Основные служебные программы и их назначение. 3.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Вариант №12 1. Периферийные устройства ПК. 2. Назовите основные принципы управления окном приложения. 2.Рассчитайте по формулам в величину значений переменных У и У1, если х изменяется от 1 до 3 с шагом 0,1.
Раздел 3. Основы математической биостатистики Вариант 1.1 1) В урне три белых и пять черных шаров. Наудачу вынимают два шара. Какова вероятность того, что эти шары разных цветов? 2) Дана плотность распределения случайной величины X :
Найти: а) константу b; функцию распределения F(x), в ответ ввести F(l/3); F(l/2); в) МХ; г) DХ; д) Р(1/3 < Х < 1/2).
Вариант 1.2 1) Игральная кость бросается шесть раз. Найти вероятность того, что число выпавших очков ни разу не повторится. 2) Изделия некоторого предприятия содержат 5% брака. Найти вероятность того, что среди пяти взятых наудачу изделий окажутся два бракованных. Вариант 3 1) В урне 2 красных, 7 зеленых , 5 синих и 10 неокрашенных шаров. Наудачу извлекается один шар. Какова вероятность того, что шар окажется окрашенным? 2) Игральная кость бросается до появления шестерки, но не более семи раз. Х–число бросаний кости. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)). 3) Изделиеие считается пригодным, если отклонение его размера от номинала не превышает по модулю 1.45 мм. Случайные отклонения X распределены нормально, причём М(Х)=0, s(Х)=1.5 мм. Определить вероятность того, что случайно взятое изделие является пригодным.
Вариант 4 1) Стрелок ведет огонь по приближающейся цели. Вероятность попадания в цель при первом выстреле равна 0.4 и увеличивается на 0.1 для каждого последующего выстрела. Какова вероятность получить два попадания при трех выстрелах? 2) Какова вероятность того, что в столбике из 100 наугад уложенных монет число монет, расположенных «орлом» вверх, находится в пределах от 45 до 55?
Вариант 5 1) На складе вперемешку хранятся лампы, полученные с четырех заводов: 250 – с первого завода, 525 – со второго, 275 –с третьего и 950 – с четвертого. Вероятность того, что лампа проработает больше 1500 часов, для продукции этих заводов соответственно равна 0.15, 0.3, 0.2 и 0.1. Найти вероятность того, что взятая наугад лампа проработает больше 1500 часов. 2) Случайная величина
Другая случайная величина связана с
Вариант 6 1) Деталь проходит три операции обработки. Вероятность получения брака на первой операции равна 0.02, на второй – 0.03, на третьей – 0.04. Найти вероятность получения детали без брака после трех операций. 2) Случайная величина
Найти a, b. Другая случайная величина связана с
Вариант 7 1) В партии из 50 изделий 6 бракованных. Из партии выбираются наудачу 5 изделий. Определить вероятность того, что среди этих пяти изделий два бракованных. 2) Задана плотность распределения вероятностей
Найти: а) константу а; б) функцию распределения F(x), в ответ ввести значения F(–1/3), F(1/3); в) М(Х), г) D(X); д) Р(–1/2 < X < 0.5).
Вариант 8 1) Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5? 2) Вероятность появления события А в каждом из 1500 испытаний равна 0.4. Найти вероятность того, что число появлений события А заключено между: а) 570 и 630, б) 600 и 660. Вариант 9 1) В урне 6 белых и 4 черных шара. Из урны наудачу извлечены 5 шаров. Найти вероятность того, что среди них 2 белых и 3 черных. 2) Случайная величина
Найти а. Другая случайная величина связана с
Вариант 10 1) Имеется две одинаковых партии изделий, содержащих по семи изделий первого сорта и по одному изделию второго сорта. Из каждой партии берут по четыре изделия. Найти вероятность того, что состав партий останется одинаковым. 2) Дана плотность распределения случайной величины X :
Найти: а) константу а; функцию распределения F(x), в ответ ввести F(1.3); F(0.5); в) МX; г) DX; д) Р(0.3 < X < 0.8). Вариант 11 1) Партия состоит из четырех изделий первого сорта и шести изделий второго сорта. Наудачу взято три изделия. Какова вероятность того, что ровно два из них одного сорта? 2) В этой задаче требуется для дискретной случайной величины X – сумма очков, выпавших при двух бросаниях игральной кости: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)). Вариант 12 1) В классе 10 мальчиков и 20 девочек. Наугад отобраны трое учащихся. Какова вероятность того, что среди них две девочки и один мальчик? 2) Дана плотность распределения случайной величины X :
Найти: параметр g; определить математическое ожидание
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 215. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
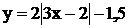 ,
, 
 ,
, 
 ,
, 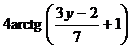
 ,
, 
 ,
, 
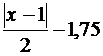 ,
, 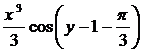
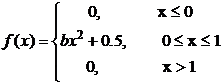
 имеет плотность распределения
имеет плотность распределения
 . Определить математическое ожидание
. Определить математическое ожидание 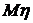 и дисперсию
и дисперсию 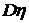 случайной величины
случайной величины  .
.
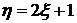 . Определить математическое ожидание
. Определить математическое ожидание 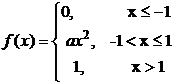
 имеет плотность распределения
имеет плотность распределения


 и дисперсию
и дисперсию  случайной величины X, функцию распределения F(x) и вероятность Р(a<Х<b). Исходные данные: a=1.5; b=3.0; a=2.0; b=2.5.
случайной величины X, функцию распределения F(x) и вероятность Р(a<Х<b). Исходные данные: a=1.5; b=3.0; a=2.0; b=2.5.