
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сформулируйте и докажите теорему о пространстве решений однородной системы линейных алгебраических уравнений.Совокупность P всех решений однородной системы уравнений является линейным пространством, которое представляет собой подпространство линейного пространства всех вектор-столбцов высоты n.
1). 2). | 48. Дайте определения вырожденной и невырожденной матриц. Приведите примеры таких матриц порядка 3 × 3 . Матрица называется невырожденной, если ее ранг = n – порядок матрицы (для квадратных матриц). Если r меньше n, матрица называется вырожденной. Строки (столбцы) вырожденной матрицы линейно зависимы. Строки (столбцы) невырожденной матрицы линейно независимы. 49. Выведите формулу умножения комплексных чисел в тригонометрической форме Возьмем два комплексных числа в тригонометрической форме.
получим для наших двух комплексных чисел формулу:
=
Т.о., для умножения z1 на z2 модули этих чисел следует перемножить, а аргументы сложить. 50. Выведите формулу деления комплексных чисел в тригонометрической форме. Возьмем два комплексных числа в тригонометрической форме.
Используя формулу деления комплексных чисел вида
получим для наших двух комплексных чисел формулу:
/учитывая основное тригонометрическое тождество, согласно которому =( /используя тригонометрические свойства косинуса и синуса суммы и разности/ = 51. Докажите, что система линейных однородных уравнений, в которой число неизвестных больше числа уравнений, имеет бесконечное число решений. Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.  Запишем общий вид однородной системы m уравнений сn неизвестными:
а21х1+ а22х2+…+ а2nхn=0 … аm1х1+ аm2х2+…+ аmnхn=0, где n>m Применим к системе метод Гаусса. В процессе преобразований не могут получиться противоречивые уравнения
т.к. все свободные члены уравнений – нули. Значит, после некоторого числа шагов мы получаем систему, где каждому уравнению будет соответствовать свое базисное неизвестное. Но поскольку число уравнений меньше числа неизвестных, то и число базисных неизвестных должно быть меньше числа неизвестных. Следовательно, обязательно имеются свободные неизвестные, а система имеет бесчисленное множество решений. | |||
| 53. Сформулируйте и докажите теорему о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений. Общее решение неоднородной системы линейных уравнений имеет вид
, где Х0 – некоторое (частное) решение неоднородной системы уравнений
- общее решение однородной системы AX=B A(X0+C1X1+C2X2+…+ CnXn)=AX0+C1AX1+…+CnAXn=AX0=B
Множество решений неоднородной системы линейных уравнений не образует линейного пространства.
54. Сформулируйте определение определителя матрицы размера ݊ × ݊. Выведите формулу для определителя треугольной матрицы. Определителем матрицы н=н будет число:
57. Дайте определение ортогональной матрицы. Докажите, что ортогональная матрица не может быть вырожденной. Квадратичная матрица называется ортогональной, если её строки образуют ортонормированную систему векторов: А*АТ=Е Доказательство. Так как QTQ = E, то |QT| |Q| = |Q|2 = 1. Значит, |Q| = ±1. По свойству определителей если определитель содержит две одинаковые строки то он равен0
| 55. Напишите формулы Крамера для решения системы линейных уравнений, состоящей из ݊ уравнений с ݊ переменными. Выведите эти формулы для случая ݊ = 2 .
 56. Дайте определение ортогональной и ортонормированной систем векторов. Докажите, что векторы ортонормированной системы векторов линейно независимы.
Система ненулевых векторов е1, е2, е3 называется ортогональной, если все ее векторы попарно ортогональны, т.е. еi * ej= 0.
Если векторы системы векторов e1, e2, ..., enпопарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (ei, ej) =0, если i ≠ j ,(ei, ei) =1.
56. Дайте определение ортогональной и ортонормированной систем векторов. Докажите, что векторы ортонормированной системы векторов линейно независимы.
Система ненулевых векторов е1, е2, е3 называется ортогональной, если все ее векторы попарно ортогональны, т.е. еi * ej= 0.
Если векторы системы векторов e1, e2, ..., enпопарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (ei, ej) =0, если i ≠ j ,(ei, ei) =1.
 58. Дайте определение подобных матриц. Докажите, что характеристические многочлены подобных матриц равны.
Определение: м. В называется подобной м. С, если существует такая невырожденная м. Т, что выполняется равенство В=Т-1СТ.
Характеристические многочлены подобных матриц равны друг другу.
В самом деле, пусть матрица Л подобна матрице В
А = Х-1ВХ.
Тогда для характеристического многочлена Л получаем
Х-1ВХ = | Х-1(λE-B)X| = | Х-1| * | λE-B| * |X|
Определители | Х-1|, |X| взаимно обратны и в произведении дают 1, поэтому:
| λE-А| = | λE-B|
что и требовалось доказать.
Из этой теоремы вытекает, в частности, что подобные матрицы
имеют одинаковые следы и определители, так как след и определитель матрицы, взятые с надлежащими знаками, являются коэффициентами ее характеристического многочлена.59. 59Дайте определение выпуклого множества. Докажите, что пересечение любого числа выпуклых множеств выпукло.
Множество F подмножества Аn называется выпуклым, если вместе с любыми двумя своими точками А и В оно содержит весь отрезок АВ.
Пересечение нескольких выпуклых множеств есть выпуклое множество.
Действительно, пусть М = М1 ∩ М2, где М1,М2 – выпуклы. Докажем выпуклость М.
Пусть А € М и В € М. Тогда А € М1 и В € М1. Так как М1 выпуклое, то это означает, что отрезок АВ содержится М1. Аналогично покажем, что АВ содержится в М2. Значит АВ содержится в М, что означает выпуклость М.
Из леммы следует, что пересечение нескольких полупространств в н-мерном пространстве Т является выпуклым множеством.
58. Дайте определение подобных матриц. Докажите, что характеристические многочлены подобных матриц равны.
Определение: м. В называется подобной м. С, если существует такая невырожденная м. Т, что выполняется равенство В=Т-1СТ.
Характеристические многочлены подобных матриц равны друг другу.
В самом деле, пусть матрица Л подобна матрице В
А = Х-1ВХ.
Тогда для характеристического многочлена Л получаем
Х-1ВХ = | Х-1(λE-B)X| = | Х-1| * | λE-B| * |X|
Определители | Х-1|, |X| взаимно обратны и в произведении дают 1, поэтому:
| λE-А| = | λE-B|
что и требовалось доказать.
Из этой теоремы вытекает, в частности, что подобные матрицы
имеют одинаковые следы и определители, так как след и определитель матрицы, взятые с надлежащими знаками, являются коэффициентами ее характеристического многочлена.59. 59Дайте определение выпуклого множества. Докажите, что пересечение любого числа выпуклых множеств выпукло.
Множество F подмножества Аn называется выпуклым, если вместе с любыми двумя своими точками А и В оно содержит весь отрезок АВ.
Пересечение нескольких выпуклых множеств есть выпуклое множество.
Действительно, пусть М = М1 ∩ М2, где М1,М2 – выпуклы. Докажем выпуклость М.
Пусть А € М и В € М. Тогда А € М1 и В € М1. Так как М1 выпуклое, то это означает, что отрезок АВ содержится М1. Аналогично покажем, что АВ содержится в М2. Значит АВ содержится в М, что означает выпуклость М.
Из леммы следует, что пересечение нескольких полупространств в н-мерном пространстве Т является выпуклым множеством.
| 77
|
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 202. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||

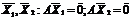

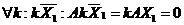



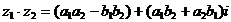 ,
, = /используя тригонометрические формулы косинуса и синуса суммы/
= /используя тригонометрические формулы косинуса и синуса суммы/

 , где z2≠0.
, где z2≠0. ,
, =
=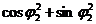 =1/
=1/ )+ (
)+ (  )i=
)i=
 а11х1+ а12х2+…+ а1nхn=0
а11х1+ а12х2+…+ а1nхn=0 , где b≠0,
, где b≠0,


 .
.

