Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема об эквивалентности пар.1. Не изменяя действия пары сил на твердое тело, ее можно перемещать в плоскости действия, поворачивать, менять модули сил, составляющих пару, и ее плечо, так чтобы момент пары не изменялся Таким образом момент пары сил {R1, R2} равен моменту исходной пары сил {P, Q}. В тоже время модули сил, составляющих эти пары разные, так же как и плечи этих пар. 2. Не изменяя действия пары сил на твердое тело, ее можно пере- мещать в другую плоскость, параллельную исходной плоскости дей- ствия. Сложение пар сил.Пусть {P1, Q1} пара сил с моментом m1, расположенная в плоскостиI, а {P2, Q2}– пара сил с моментом m2, расположенная в плоскости II.Эти плоскости пересекаются по прямой АВ. Так как пару можно перемещать в плоскости действия, то можно добиться того, чтобы силы,составляющие пары были приложены в точках А и В.В точке А приложены силы P1 и P2, их можно заменить равнодействующей R1. Силы Q1 и Q2, приложенные в точке В, можно заменить равнодействующей R2. Силы R1 и R2 образуют пару, так как по построениюони равны по модулю и действуют вдоль параллельных прямых в разные стороны. Вычислим момент этой пары.m(R1, R2) = AB × R2 = AB ×(Q1 + Q2) = AB × Q1 = AB × Q2 = m1 + m1.Таким образом при сложении двух пар сил получается пара, вектор момент которой равен сумме вектор моментов исходных пар.
9. Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сумме всех сил системы, и главный момент, равный геометрической сумме моментов всех приводимых сил относительно центра приведения (рис. 1.33). Сложим  Затем векторно сложим векторы моментов
Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от вы-бора центра приведения. По модулю главный вектор вычисляется Где
проекции главного вектора на координатные оси Направление находим по направляющим косинусам
Главный момент
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из координатных осей равнялась нулю, и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю.
Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения явля-ются уравнениями равновесия параллельных сил в пространстве (рис. 1.34).
Для параллельных сил расположенных в плоскости XOY (рис. 1.35), имеем два уравнения равновесия: Теорема Пуансо: Не изменяя действие силы на тело её можно перенести в любую точку тела добавив при атом пару сил с моментом, равным моменту переносимой силы относительно новой точки приложения.
10. Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил (рис.). Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия: Условия равновесия плоской системы сил.
Для плоской системы сил условия равновесия будут частным
, определяющих условия равновесия пространственной системы сил. Например, если силы расположены в плоскости Оху, то аналитические условия равновесия можно записать в виде: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма алгебраических моментов этих сил относительно любого центра О были равны нулю. Алгебраическим моментом силы относительно точки называют момент силы относительно оси, проходящей через данную точку перпендикулярно плоскости, в которой расположена сила и точка Вместо иногда удобно применить условия равновесия в виде уравнений трех моментов: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю:
Необходимость утверждения следует из того, что третье условие равенствам
13. Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Рассмотрим систему сил , , Для доказательства теоремы найдем соответствующие выражения моментов m0( Обозначим равнодействующую сил ,
14. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 646. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и т.д., получим силовой многоугольник, где
и т.д., получим силовой многоугольник, где 

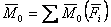


 *(Rx, Ry, Rz), а проекции каждой из сил
*(Rx, Ry, Rz), а проекции каждой из сил  (X1, Y1 , Z1),
(X1, Y1 , Z1),  (X2, Y2, Z2) и т.д.
(X2, Y2, Z2) и т.д.


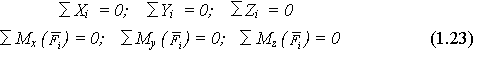




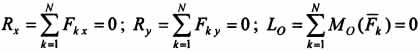
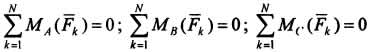


 …,
…,  , сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.
, сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О. ), m0(
), m0(  . Но, как видно из рисунка, ,
. Но, как видно из рисунка, ,  где F1x - проекция силы на ось Ох; следовательно
где F1x - проекция силы на ось Ох; следовательно  Аналогично вычисляются моменты всех других сил.
Аналогично вычисляются моменты всех других сил. , где
, где  . Тогда, по теореме о проекции суммы сил на ось, получим
. Тогда, по теореме о проекции суммы сил на ось, получим  . Умножая обе части этого равенства на ОА, найдем:
. Умножая обе части этого равенства на ОА, найдем:  или
или