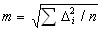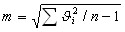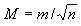Виды погрешностей измерений. Свойства случайных погрешностей

Приборные, внешней среды, личные, Грубые погрешности.

По своему характеру и свойствам различают погрешности грубые, систематические и случайные.Случайными называют такие погрешности, которые при повторных измерениях изменяются случайным образом. Вызванные непрерывными изменениями условий измерений случайные погрешности неизбежны. Определить заранее их величину и знак невозможно, поэтому нет возможности освобо­дить от них результаты измерений.

Свойства случайных погрешностей. Пусть величина, истинное значение которой X, многократно измерена и получено п результатов измерений 1\, /2, ..., 1п- Если измерения одной и той же величины выполнены в одинаковых условиях (одними и теми же приборами и методами, одним лицом при одинаковых внешних условиях), то результаты измерений считают равноточными. Из накопленного опыта известно, что при достаточно большом числе измерений одной и той же величины ряд случайных погрешностей равноточных измерений

Ai=^i — Х\ Ь2=12-Х; Ап = 1п-Х обладает следующими свойствами: 1) по абсолютному значению погрешности не превышают некоторого известного предела, т. е. |А|^Апред. Значение этого предела зависит от условий измерений; 2) малые по абсолютному значению погрешности встречаются чаще больших; 3) положительные погрешности встречаются так же часто, как и отрицательные; 4) среднее арифметическое из случайных погрешностей равноточных измерений при неограниченном возрастании числа измерений стремится к нулю:

lim [(Ax -f Д2-f ... -f Дя)/я] = 0. Последнее свойство (свойство компенсации), являющееся следствием первых трех, распространяется и на произведения независимых случайных погрешностей Л*, А3, поскольку такие произведения, очевидно, обладают всеми вышеназванными свойствами случайных погрешностей, т. е.

lim /J =0, (3.6)

fe->oo k

где k — число произведений.

11. Арифметическая середина. Средняя квадратическая, предельная и относительная погрешностиНаилучшим критерием оценки точности  измерений принято считать среднюю квадратическую погрешность (СКП) измерения, определяемую по формуле Гаусса:  

где Δi=li-X (Х - истинное значение измеряемой величины, а li - результат измерения).

Так как, в большинстве случаях истинное значение неизвестно, то СКП определяют по формуле Бесселя:

где ϑi=li-х (х - средняя арифметическое значение или вероятнейшее значение измеряемой величины, а li - результат измерения).

СКП арифметической середины:

Эта формула показывает, что СКП арифметической середины в √n раз меньше СКП отдельного измерения.На практике различают предельные и относительные погрешности. Теорией доказывается, а практикой подтверждается, что абсолютное большинство случайных погрешностей находится в интервале от 0 до m - 68% , от 0 до 2m - 95% , от 0 до 3m - 99.7%.

На практике за предельную погрешность принимают 2m, т.е. с вероятностью 95% можно утверждать, что случайные погрешности не превысят величины равной 2m. Если n<10 то ϑi(пред)=tB . M, где tB - коэффициент Стьюдента (таблица).

Рассмотрим на примере как выполняется математическая обработка результатов ряда равноточных измерений. Пусть длина линии измерена шесть раз (см. таблицу). Необходимо найти вероятнейшее значение измеренной величины и оценить результаты измерений.

l'=75.10 м,

x =75.10+0.37/6=75.16 м,

m =√91 / 5=4.2 см,

М = 4.2 / √6=1.7 см,

ϑi(пред)=tB . M = 2.52 . 1.7 = 4.4 см,

L = 75.16 + 0.04 м (P=95%),

Отн.погр.ΔL/L=4.4/7510=1/1700