
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фотоны. Фотоэлектрический эффект
6.1 Энергия где Единица измерения энергии 1 эВ = 6.2 Формула Эйнштейна для внешнего фотоэффекта:
где
6.3 Фотоэффект наблюдается, если
где 6.4 Кинетическая энергия фотоэлектронов связана с задерживающей разностью потенциалов Uз следующей зависимостью: Tmax = eUз, где e – заряд электрона, 6.5 Максимальная кинетическая энергия электрона в нерелятивистском и релятивистском случаях выражается различными формулами: · если фотоэффект вызван фотоном, имеющим энергию много меньшую энергии покоя электрона ( т.е.
· если фотоэффект вызван фотоном, обладающим энергией порядка или больше энергии покоя электрона (т.е.
Пример 8. Определить «красную» границу 
Дано: Найти: Решение. При облучении металла светом, длина волны Учитывая, что
Работу выхода для цезия определим из уравнения Эйнштейна:
Отсюда Выполним вычисления, подставив в формулу (1) числовые значения величин:
Ответ:
Эффект Комптона
7.1 Изменение длины волны фотона где m0 – масса электрона отдачи; 7.2 Импульс фотона:
7.3 Комптоновская длина волны:
При рассеянии фотона на электроне
7.4 Энергия покоя электрона:
7.5 При комптоновском рассеянии закон сохранения имеет вид:
где Если эффект Комптона вызван фотоном, имеющим энергию много меньшую энергии покоя электрона, то можно пользоваться нерелятивистким выражением для кинетической энергии. В противном случае следует пользоваться формулами релятивистской механики.
Пример 9. Фотон с энергией 0,500 МэВ рассеялся на свободном электроне под углом 600. Найти энергию рассеянного фотона, кинетическую энергию и импульс электрона отдачи.
Дано: Найти: Решение. 1. Энергию рассеянного фотона найдем, воспользовавшись формулой Комптона: Выразим длины волн через энергии фотона: Подставив выражения для длин волн (2) в (1), получим:
Разделим обе части этого равенства на hc: Обозначив энергию покоя электрона m0c2 через Е0, получим: Подставим числовые значения энергий фотона и электрона, выполним вычисления:
1. Кинетическую энергию электрона отдачи Т определим из закона сохранения энергии: Отсюда выразим Т = 0,500 – 0,335 = 0,165 МэВ. 2. Импульс электрона отдачи найдем из закона сохранения импульса
где Модули импульсов фотонов выразим через их энергии:
Зная
Выполним вычисления, подставив числовые значения в единицах СИ (1 МэВ = =1,6
Проверим размерность:
Для определения направления импульса рассеянного фотона найдем угол По теореме синусов:
отсюда
Заменив импульс рассеянного фотона соотношением
Вычислим
Ответ:
Давление света
8.1 Давление, производимое светом при нормальном падении:
где Ее – облученность поверхности ( 8.2 Количество лучистой энергии
где Sn – площадь поверхности, перпендикулярной к потоку энергии; Фе – поток лучистой энергии; N – число фотонов, падающих на поверхность Sn за время 8.3 Объемная плотность энергии излучения: где n – концентрация фотонов в пучке (
Пример 10. Пучок параллельных лучей монохроматического света с длиной волны
Дано: Найти: F; Решение. 1. Определяем силу светового давления F на поверхность S: F = pS. (1)
Световое давление р можно найти по формуле: Подставляя формулу (2) в формулу (1), получим: Произведение Ее на S есть величина, численно равная энергии, падающей на данную площадку в единицу времени, то есть поток излучения Фе равен Фе = ЕеS. С учетом этого формула (3) примет вид:
Вычислим силу давления F (значение скорости света в вакууме берем из Приложения ,
1. Произведение энергии
Так как Отсюда
Подставляем числовые значения (значения постоянной Планка берем из Приложения,
Проверим размерность:
Ответ: F = |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 647. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , масса m и импульс p фотона выражаются соответствующими формулами:
, масса m и импульс p фотона выражаются соответствующими формулами: ;
; ;
; ,
, – частота излучения;
– частота излучения;  – длина волны в вакууме; с – скорость света в вакууме; h – постоянная Планка,
– длина волны в вакууме; с – скорость света в вакууме; h – постоянная Планка,  .
. .
. или
или  ,
, ; А – работа выхода электрона из данного металла; Т – максимальная кинетическая энергия фотоэлектронов,
; А – работа выхода электрона из данного металла; Т – максимальная кинетическая энергия фотоэлектронов, .
. > A, и не наблюдается при
> A, и не наблюдается при  определяет “красную” границу фотоэффекта:
определяет “красную” границу фотоэффекта: ;
;  ,
, – минимальная частота, при которой еще возможен фотоэффект в данном металле;
– минимальная частота, при которой еще возможен фотоэффект в данном металле;  – максимальная длина волны, соответствующая частоте
– максимальная длина волны, соответствующая частоте  .
. .
. 0,51 МэВ, где m0 – масса покоя электрона, с – скорость света), то можно воспользоваться нерелятивистским выражением для кинетической энергии электрона:
0,51 МэВ, где m0 – масса покоя электрона, с – скорость света), то можно воспользоваться нерелятивистским выражением для кинетической энергии электрона: ,
, 0,51 МэВ), то следует пользоваться релятивистским выражением для кинетической энергии электрона:
0,51 МэВ), то следует пользоваться релятивистским выражением для кинетической энергии электрона: .
.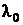 фотоэффекта для цезия, если при облучении поверхности фиолетовым светом длиной волны
фотоэффекта для цезия, если при облучении поверхности фиолетовым светом длиной волны  фотоэлектронов равна 0,65 Мм/с.
фотоэлектронов равна 0,65 Мм/с. м/с/; m = 9,1
м/с/; m = 9,1  кг,
кг, 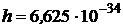 Дж·с;
Дж·с;  м/с (данные m, h, c взяты из Приложения).
м/с (данные m, h, c взяты из Приложения). .
. , получим:
, получим: ,
,  .
. .
. . (1)
. (1) нм.
нм. при рассеянии его на свободном электроне в металле на угол
при рассеянии его на свободном электроне в металле на угол  определяется:
определяется: или
или  ,
, – длины волн фотона до и после рассеяния соответственно; с – скорость света в вакууме.
– длины волн фотона до и после рассеяния соответственно; с – скорость света в вакууме. .
. .
. = 2,436 пм.
= 2,436 пм. МэВ.
МэВ.
 - энергии фотона до и после рассеивания соответственно, Т - кинетическая энергия электронов отдачи.
- энергии фотона до и после рассеивания соответственно, Т - кинетическая энергия электронов отдачи. МэВ,
МэВ,  = 600, Е0 = 0,511 МэВ (энергия покоя электрона).
= 600, Е0 = 0,511 МэВ (энергия покоя электрона). , Т,
, Т,  .
. . (1)
. (1) ;
;  ;
;  . (2)
. (2) .
. .
. .
.  МэВ
МэВ
 и подставим числовые значения, получим:
и подставим числовые значения, получим: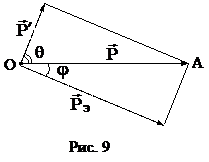 (рис. 9):
(рис. 9):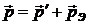 ,
, и
и  – импульсы падающего и рассеянного фотонов;
– импульсы падающего и рассеянного фотонов;  – импульс электрона отдачи.
– импульс электрона отдачи. ;
;  .
. ,
,  и угол
и угол  (рис. 9), можно определить рэ по теореме косинусов:
(рис. 9), можно определить рэ по теореме косинусов:
 Дж):
Дж): кг ·м/с.
кг ·м/с. .
. (рис. 9).
(рис. 9). ,
, .
. , получим:
, получим: .
. :
: ;
;  = 0,335 МэВ; Т = 0,165 МэВ; рэ = 0,235
= 0,335 МэВ; Т = 0,165 МэВ; рэ = 0,235  ;
;  = 410.
= 410. ,
, ,
, - энергия всех фотонов, падающих на единицу площади за единицу времени); с – скорость распространения электромагнитного излучения в вакууме;
- энергия всех фотонов, падающих на единицу площади за единицу времени); с – скорость распространения электромагнитного излучения в вакууме; 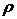 – коэффициент отражения;
– коэффициент отражения;  – объемная плотность энергии излучения (
– объемная плотность энергии излучения (  ).
). , падающей на поверхность Sn за время
, падающей на поверхность Sn за время  :
: ,
, ;
;  ,
, ),
),  = 663 нм падает нормально на зеркальную плоскую поверхность. Поток излучения Фе=0,6 Вт. Определить: 1) силу давления F, испытываемую этой поверхностью; 2) число фотонов
= 663 нм падает нормально на зеркальную плоскую поверхность. Поток излучения Фе=0,6 Вт. Определить: 1) силу давления F, испытываемую этой поверхностью; 2) число фотонов  , ежесекундно падающих на поверхность.
, ежесекундно падающих на поверхность. м; Фе = 0,6 Вт;
м; Фе = 0,6 Вт;  .
.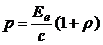 . (2)
. (2) (3)
(3) .
. Н.
Н. .
.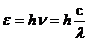 , то
, то  .
. .
. ):
): с-1.
с-1. .
. Н,
Н,  с-1.
с-1.