
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕРМОДИНАМИЧЕСКИЙ И КИНЕТИЧЕСКИЙ АСПЕКТЫ ДИФФУЗИОННОГО ПЕРЕМЕЩЕНИЯ АТОМОВНа первый взгляд кажется, что привлечь термодинамику для описания диффузии невозможно из принципиальных соображений. Действительно, термодинамика - наука о равновесии. Законы термодинамики применимы к макроскопическим системам, находящимся в состоянии равновесия. Определение понятия «термодинамическое равновесие» включает, в частности, требование, чтобы через систему не проходили никакие потоки. А диффузия связана с переносом массы и является процессом, существенно необратимым. В состоянии равновесия диффузионные потоки должны исчезать. Тем не менее термодинамическое описание - как способы подхода к явлению, так и способы расчета параметров – оказалось чрезвычайно полезным для рассмотрения диффузионного перемещения атомов, а связи между термодинамикой и теорией диффузии достаточно многообразными. Это многообразие диктуется несколькими обстоятельствами: 1. Диффузионное перемещение тесно связано с наличием в кристалле дефектов, в первую очередь вакансий. Как уже отмечалось, коэффициент диффузии пропорционален концентрации вакансий. Расчет равновесной концентрации вакансий – типичная задача термодинамики, поскольку эту концентрацию находят из условия минимума свободной энергии кристалла. Аналогично можно оценить концентрацию более сложных дефектов: бивакансий, комплексов вакансия-атом (или атомы), примеси и т. д. Даже если в кристалле имеются неравновесные вакансии, термодинамика весьма облегчает анализ ситуации, ибо помогает оценить их количество, если известна предыстория образца, и разобраться в направлении возникающих вакансионных потоков. Термодинамика утверждает, что вакансии перемещаются в участки, где их химический потенциал (парциальная молярная свободная энергия) имеет наименьшее значение. Построив соответствующие модели (например, учитывая энергию упругих напряжений), можно оценить работу перемещения вакансий и мощность возникающих вакансионных потоков.  2. Связь между диффузионными характеристиками и термодинамическими свойствами системы предлагает теория абсолютных скоростей реакций. Согласно этой теории диффузионный скачок соответствует переходу через некоторый барьер (переходное состояние), в котором перескакивающий атом находится в равновесии с остальной решеткой. Благодаря такому подходу оказывается возможным применение и термодинамических, и статистических методов расчета. На этих же предположениях основаны все попытки учета кооперативного характера диффузионного скачка. Последовательное развитие модели переходного состояния позволяет искать связи между диффузионными параметрами (энергия активации, предэкспонента) и термодинамическими свойствами системы (теплота испарения, температура плавления, различные характеристические температуры, упругие модули и т. д.). Удовлетворительное (в большинстве случаев) совпадение предсказаний теории с экспериментом оправдывает предположения, лежащие в основе теории, хотя априорно они кажутся недостаточно обоснованными. 3. Теория Онзагера позволила построить весьма общую феноменологическую схему, включающую многокомпонентные системы, перемещение неравновесных дефектов, диффузию в поле сил, диффузию при наличии иных градиентов, кроме градиента концентрации, и т. п. Столь общий подход создал основу для анализа границ применимости некоторых существующих описаний (например, уравнений Фика, Даркена и других). Таким образом, термодинамика представляет прочный каркас, на котором строится современная теория диффузии. Вместе с тем такое описание, будучи чрезвычайно общим, не позволяет достаточно четко выяснить физический смысл возникающих параметров (энтальпии или энергии активации, энтропийных множителей, теплота переноса и т. д.). В некоторых случаях (многокомпонентные системы, совокупное действие нескольких полей) для определения всех коэффициентов даже не удается указать достаточного количества практически осуществимых экспериментов. Это вообще характерно для термодинамического описания; конкретные механизмы лежат за его пределами. Задача расчета коэффициентов, определяющих диффузионный поток, в рамках конкретных моделей - задача кинетики. Статистические методы позволяют связать диффузионные параметры с характеристиками атомов и молекул, а теория строения вещества - рассчитать эти характеристики. Диффузионные параметры можно также найти из опыта путем непосредственного измерения скорости процесса при различных температурах. Вместе с тем такого статистико-термодинамического описания недостаточно. Хотя диффузионное перемещение в той или иной форме включает в себя полный или частичный разрыв связей между перескакивающим атомом и соседями, однако опыт показывает, что для анализа диффузионной подвижности в реальных сплавах и в реальных условиях знания равновесных характеристик, т. е. величин энергий связей, мало. Необходима более детальная информация о характере связей, возникающих между различными атомами и между атомами и дефектами, их пространственном распределении «направленности». Физически ясно, что «жесткие», направленные связи менее благоприятны для диффузии, чем «гибкие», ненаправленные. Тип и свойства возникающих связей определяются в первую очередь электронной структурой атомов и дефектов, тесно связанной с их расположением в кристалле - структурой реального кристалла. Недостаточно также знать равновесную концентрацию дефектов в системе. Необходимо иметь сведения о пространственном распределении дефектов (например, вакансий), которые могут быть локализованы в тех или иных областях кристалла. Необходимо иметь информацию о влиянии на диффузионную подвижность неравновесных дефектов, следовательно, и о причинах их возникновения, их устойчивости (релаксационных свойствах), взаимодействии с источниками и стоками, возможности возникновения различных ассоциаций дефектов и т. д. Иначе говоря, диффузионное перемещение тесно связано со структурой твердого тела, с наличием в нем дефектов и весьма существенно зависит от их типа, количества, расположения и перемещения. Простейшей и убедительной иллюстрацией является самодиффузия. Отношение энергии активации самодиффузии к теплоте испарения для металлов с данным типом решетки является величиной приблизительно постоянной. В этом соотношении проявляется термодинамический фактор. Однако во многих случаях энергия активации меняется значительно сильнее, чем теплота испарения. Так, при плавлении энергии активации самодиффузии меняется более чем на порядок, а теплота испарения - очень мало. Еще более ярким является влияние малых количеств примесей на самодиффузию растворителя. Это влияние - следствие кинетического фактора, так как термодинамические свойства растворителя практически остаются постоянными. Подвижность атомов растворителя изменяется в результате того, что в окрестности их возникают искажения решетки (если атомные объемы примеси и растворителя заметно отличаются) или искажения электронной плотности (при заметном отличии электронного распределения) или же по каким-либо другим «структурным» причинам. Как следствие, самодиффузия происходит в неоднородной среде, содержащей области разной подвижности, и эффективный коэффициент диффузии может существенно измениться. Точно так же нельзя понять быструю диффузию по границам зерен на основе термодинамики, не привлекая кинетических факторов, структурных аргументов. Отличие энергии атомов в границе от их энергии в теле зерна недостаточно велико, чтобы объяснить огромное отличие коэффициентов диффузии (на несколько порядков при температурах около 0,6-0,7 Тпли больше - при более низких температурах) . Таким образом, скорость диффузии подвержена воздействию как термодинамического (изменение энергии связи, активности и других термодинамических свойств), так и кинетического (изменение подвижности за счет изменения атомной и электронной структуры) факторов. Поэтому совместное привлечение обоих подходов представляется наиболее рациональным способом обсуждения основных идей теории диффузии, результатов диффузионных измерений, связей между диффузионными характеристиками и свойствами материалов. Вместе с тем следует иметь в виду, что указанные связи весьма сложны для анализа, и к полученным при таком анализе результатам следует относиться с известной осторожностью. Термодинамические соотношения, которыми мы пользуемся для описания диффузии, всегда носят макроскопический характер. Элементарный же акт диффузии развивается в микроскопических пространственно-временных масштабах. Многие предположения, которые делаются при анализе (например, о равновесии между перескакивающим атомом и решеткой), недостаточно обоснованы. Что же касается моделей, применяемых для расчета кинетических коэффициентов, то область их применимости, естественно, ограничена, поскольку многие факторы, особенно структурные, не поддаются детальному учету. Поэтому, хотя теоретический анализ приводит в большинстве случаев к результатам, согласующимся с экспериментами и даже позволяющим делать некоторые предсказания, однако всегда можно ждать, что появится экспериментальный факт, противоречащий этим результатам. И не следует, по-видимому, особенно удивляться, если такие экспериментальные факты действительно появляются.
Лекция 2-3 МАКРОСКОПИЧЕСКОЕ ОПИСАНИЕ ДИФФУЗИИ План 1.1-е уравнение Фика. Коэффициент диффузии. Разные типы коэффициентов диффузии. 2. Влияние симметрии кристалла на коэффициенты диффузии. Принцип Немана. 3. 2-е уравнение Фика. Частные решения 2-го уравнение Фика. 4.Концентрационная зависимость коэффициента диффузии. Метод Матано-Больцмана. 1 В физике диффузии сформировалось два подхода к рассмотрению явления диффузии: макроскопический и микроскопический подходы, которые, дополняя друг друга, помогают создать объективные представления об этом сложном явлении. Диффузия воспринимается обычно как процесс перераспределения вещества в пространстве с течением времени. Хотя это перераспределение происходит благодаря элементарным микроскопическим перемещениям частиц вещества, результат большого числа таких перемещений носит макроскопический характер. При макроскопическом подходе тело, в котором протекает диффузия, рассматривается как сплошная среда – континуум, и основным уравнением, описывающим поведение этой среды является уравнение непрерывности:
где В однородной многокомпонентной системе поток атомов данного компонента представляет собой векторную величину, численно выражающую количество вещества данного компонента, пересекающее в единицу времени единичную площадку, перпендикулярную вектору потока. Выражение доя потока произвольно выбранного компонента k имеет вид:
где
Выражение, получаемое из (1.2 ) при
Для одномерной задачи: Уравнения (1.2 ) – (1.4 ) описывают перенос вещества в определенном направлении вследствие диффузии. Происхождение члена, содержащего скорость Типы коэффициентов диффузии В зависимости от условий проведения диффузионного опыта различают несколько типов коэффициентов диффузии. При этом любой из них вводится в соответствии с 1 законом Фика как коэффициент пропорциональности между потоком и градиентом концентрации. Но диффузионный поток можно определить по-разному, выбрав систему отсчета. Для кристаллических твердых тел существуют две наиболее удобные системы отсчета: лабораторная, связанная с концами образца (при этом изменением размера образца пренебрегают) и решеточная, жестко связанная с атомными плоскостями. Решеточную систему координат можно отметить инертной меткой (тонкой проволокой, частицами оксида, царапинами ). Эти инертные метки не вносят вклада в диффузию, а только «следят» за движением соседних атомных плоскостей. Потоки, измеренные относительно лабораторной системы отсчета, обозначим через j’, а относительно подвижной, решеточной – j. При контакте двух образцов А и В , неограниченно растворимых в твердом состоянии, происходит перемешивание вследствие взаимной диффузии обоих компонентов. Пусть j’- поток, измеренный относительно края образца. Если диффузия происходит по оси Х, то
где Если размер кристалла и его плотность в процессе опыта не изменяются, то Подвижность каждого компонента можно охарактеризовать собственным коэффициентом диффузии, который совпадает с коэффициентом взаимной диффузии только, если собственные коэффициенты диффузии обоих компонентов равны между собой. В противном случае каждая плоскость решетки в диффузионной зоне движется относительно лабораторной системы координат в сторону компонента с большим собственным коэффициентом диффузии – возникает «течение» решетки как целого. Тогда можно записать связь между потоками в неподвижной j’ и подвижной j системах координат:
где Собственный коэффициент диффузии i-того компонента
Наглядную аналогию между собственным коэффициентом диффузии и коэффициентом взаимной диффузии предложил Шьюмон. Пусть на поверхности воды в реке вылили пузырек чернил. Чернила расплываются и одновременно сносятся течением. Поэтому наблюдатели в лодке и на берегу зафиксируют разную скорость расплывания чернил. Правильное представление о собственной диффузии чернил составит движущийся наблюдатель. В отсутствие внешних сил, если Подвижность i-того компонента можно охарактеризовать парциальными коэффициентами диффузии Парциальные коэффициенты можно определять как для собственной, так и для взаимной диффузии. Для взаимной диффузии их нужно вводить через поток Как следует из выражения (1.7), есть диагональные коэффициенты диффузии В бинарной системе Таким образом, если все Все эти коэффициенты диффузии являются коэффициентами гетеродиффузии или химической диффузии. Под гетеродиффузией понимают процесс диффузионного перемешивания разнородных атомов, возникающего в связи с отличиями имеющихся концентраций от равновесных. Самодиффузия представляет собой диффузионное перемешивание атомов, происходящее и в отсутствие градиента концентрации, как выравнивание изотопного состава. При самодиффузии направленный поток атомов можно получить при наличии градиента напряжений или градиента химического потенциала. 2 Принцип Неймана Симметрия кристаллической решетки образца, исследуемого при диффузии, накладывает ограничения на компоненты тензора коэффициентов диффузии. Эти ограничения подчиняются принципу Неймана, который утверждает: если преобразование координат входит в группу преобразований симметрии кристалла, то тензор коэффициентов диффузии остается при таком преобразовании инвариантным. Рассмотрим два вектора
где различные скалярные потоки направлены параллельно трем осям прямоугольной системы координат. Совокупность девяти чисел, обозначенных Рассмотрим кубик материала с кубической решеткой. Пусть этот кубик – монокристалл с осями, перпендикулярными граням куба. Систему координат сцепим с этими осями и выберем градиент концентрации так, что
Если считать, что градиент направлен по оси y , т.е.
Так как решетка кубическая, то ось х Аналогично ось z В решетке с тетрагональной симметрией направления В ромбической решетке все направления Пока что мы не принимали во внимание
Предположим теперь, что источник и сток, создававшие градиент удалены, а кристалл повернут на 180°. Так как
для кубической системы для тетрагональной и гексагональной систем │ для ромбической системы │ Например, определяем коэффициент диффузии в тетрагональном или гексагональном кристалле с помощью „меченных” атомов. Если монокристалл имеет ось с – ось симметрии шестого порядка, перпендикулярную одной из граней, то метку (радиоактивный изотоп) можно нанести на эту грань. Градиент концентрации параллелен оси с и поток тоже, так как Для промежуточного случая, когда плоскость с нанесенным слоем изотопа составляет угол (90°-
3. 2-е уравнение Фика. Частные решения 2-го уравнение Фика
В отсутствие источников и стоков (химическая реакция, фазовое превращение, испарение и т. д.) можно считать, что количество диффундирующего вещества остается постоянным; вещество при диффузии только перераспределяется. Второе уравнение Фика описывает изменение концентрации диффундирующего вещества в пространстве и во времени. Это уравнение непосредственно следует из баланса вещества при диффузии и выражения для потока. Рассмотрим одномерную задачу: концентрация зависит только от х. Вычислим количество вещества, протекающее через две плоскости х и x+dx, находящиеся на расстоянии dx одна от другой. Через плоскость х проходит количество вещества, которое составляет в соответствии с І уравнением Фика - -DS
Учитывая, что
Подставив в (1.13 ) выражение для dq (1.12 ), получим 2-е уравнение Фика:
Для трехмерной задачи, кoгдa концентрация зависит от всех трех координат, второе уравнение диффузии принимает вид
Уравнение (1.13) легко получить из 1-го уравнения Фика, если записать закон сохранения вещества при диффузии в форме уравнения непрерывности для потока:
Подставляя в (1.14) выражение для плотности потока, получим 2-е уравнение Фика с коэффициентом диффузии, зависящим от координат:
Второе уравнение диффузии представляет собой дифференциальное уравнение в частных производных, и для его решения необходимо сформулировать начальные и граничные условия, которым должна удовлетворять концентрация диффундирующего вещества. Эти условия определяют на основе анализа обстановки, в которой происходит процесс диффузии. Предполагается, что внутри твердого тела концентрация является непрерывной функцией координат и времени; ее первая производная по t , первыe и вторые производные по х, y, z также непрерывны. Эти предположения не применимы для поверхности твердого тела, а также для внутренних границ раздела и некоторого момента времени, с которого начинается поступление диффундирующего вещества: в этих точках и в этот момент времени концентрация и ее производные могут претерпевать разрыв. Начальное распределение концентраций с (х,у,z,0) может быть произвольным, но чаще всего эта функция постоянна либо равна нулю. Что касается граничных условий (условий на поверхности), то обычно в задачах диффузии задана либо концентрация на поверхности с(0, t),либо поток ( Уравнение диффузии (в математике его чаще называют уравнением теплопроводности) решают различными методами; основными являются метод разделения переменных (Фурье), операционный метод (Лапласа - Карсона - Хевисайда), метод источника (функций Грина). Наиболее часто встречаются следующие решения 2-го уравнения Фика: 1. Истокообразное решение: 2. Решение в виде функции ошибок: Функцию ошибок (встречаются также термины интеграл вероятности, функция Крампа) - error function определяют следующим образом:
Решения в виде функции ошибок чаще всего используют в задачах диффузии в неограниченное или полуограниченное тело через поверхность, на которой поддерживается постоянная концентрация. 3. Решение в виде экспонент: простое дифференцирование показывает, что выражение Вехр(DА2t Для ограниченных задач решение обычно имеет вид суммы экспонент с действительной частью по времени и комплексной по координате. Второй множитель чаще представляют в виде тригонометрических функций синусов и косинусов. 4. Решение для стационарного состояния: если концентрация не зависит от времени, то решение уравнения(1.14) имеет вид с=ах+b, где а и b-постоянные. Обсудим теперь, какие граничные условия обычно встречаются в диффузионных задачах. Имеется в виду граница (поверхность) раздела между образцом, в котором происходит диффузия, и окружающей средой, из которой вещество поставляется в образец или в которую оно может переходить. На границе раздела происходит какой-либо «кинетический» процесс: адсорбции, химическая реакция, сублимация и т. д. Cкорость такого процесса характеризуется кинетической константой k. Для описания скорости суммарного процесса следует ввести эффективный коэффициент диффузии: Тогда возможны две предельные ситуации: первая, когда диффузия протекает медленно или велики пути диффузии, во всяком случае Второй предельный случай возникает, если диффузия происходит быстро или диффузионные пути малы: На практике обычно приходится иметь дело со смешанной кинетикой. Тогда следует пользоваться граничными условиями типа В, когда на поверхности происходит массообмен с окружающей средой по некоторому закону, чаще всего линейному. Так, если на поверхности происходит химическая реакция первого порядка, то поток вещества через поверхность пропорционален разyости концентраций между поверхностью (с)и окружающей средой (со);тогда граничные условия можно записать в виде -D( Рассмотрим решения второго уравнения Фика (1.14) с коэффициентом диффузии, не зависящим от координат, для различных частных случаев. Если это не оговорено специально, то рассматривается одномерная задача. І. Диффузия в неограниченный образец (- 1. Из бесконечно тонкого слоя (мгновенный источник мощностью q в точке х0): В частном случае, когда х0=0
Концентрационные кривые, описывающие зависимость концентрации от положения (координаты х) для различных моментов времени, приведены на рис. 1.
Площадь под кривой в любой момент времени равна q. С течением времени кривые расплываются, а максимум понижается по закону t-1/2. Концентрация вещества, распространяющегося по плоскости из точечного источника в точке r=0, на расстоянии r от источника в момент времени t описывается выражением Аналогичное выражение для точечного источника в объеме имеет вид
2. Диффузия из слоя конечной толщины (-а<х<а),содержащего в начальный момент диффундирующее вещество с постоянной концентрацией (с0)(при
На рис. 2 приведены некоторые численные значения величины с/с0, полученные из выражения ( ) при различных значениях параметра Dt/a2.
ІІ Диффузия в полуограниченный образец (0<х< 1. Диффузия в полуограниченный образец из другого полуограниченного образца (-
2. Через поверхность (х=0), на которой поддерживается постоянная концентрация с0, не зависящая от времени с(0,t)=с0:
Обратной этой является задача диффузии из полуограниченного образца с начальной концентрацией с0 через поверхность (х=0) в среду, не содержащую диффундирующего вещества, так что на поверхности всегда имеется нулевая концентрация с(0, t)=0:
Количество вещества, прошедшего через единицу поверхности за время t, проще всего найти как интеграл по времени от потока. т.е.
При постановке эксперимента и обработке экспериментальных данных важно, чтобы выбранное решение в наибольшей степени соответствовало граничным условиям опыта. Чаще всего затруднения возникают при решении вопроса, является ли образец ограниченным или бесконечным (полубесконечным) в диффузионном смысле и диффундирует ли вещество из бесконечного тонкого слоя или слой этот имеет конечные размеры. В обоих случаях ответ на вопрос определяется сравнением так называемого диффузионного пути (lдиф, т.е. среднего расстояния, которое проходит диффундирующая частица за время опыта) с размером образца (1) в первом и толщиной слоя (а) во втором случаях. Мы увидим ниже, что lдиф ≈ Если Такую оценку не всегда можно сделать, поскольку во многих задачах неизвестен коэффициент диффузии, и его определение как раз и является целью эксперимента. Тогда следует прибегать к косвенным оценкам своим для каждой конкретной задачи. Например, если из стальной пластины при отжиге удаляется азот, и за время опыта пластина теряет 90% первоначально содержавшегося в ней азота, то ясно, что следует пользоваться решением диффузионной задачи для ограниченного образца.
4 Концентрационная зависимость коэффициента диффузии. Метод Матано-Больцмана Все рассмотренные до сих пор решения 11 уравнения Фика справедливы только для постоянного коэффициента диффузии. В реальных опытах коэффициент взаимной диффузии, как и парциальные коэффициенты диффузии в сплаве, существенно зависит от концентрации компонентов. В этом случае 11 уравнение Фика:
нельзя свести к виду
а требуется найти некий нестандартный способ его решения. Запишем 2-е уравнение Фика (одномерный случай) для относительной концентрации в виде:
решение уравнения (1.22) можно найти, используя подстановку Больцмана. Больцман предложил ввести новую переменную
Матано предложил специальную методику нахождения Математический смысл метода заключается в том, что если начальные и граничные условия, которым удовлетворяет уравнение (1.22), можно выразить через новую переменную Этот метод позволяет рассчитать зависимость На рис. слева от границы раздела до начала опыта с= с= Поскольку в соответствии с условиями применимости метода координата х плоскости с произвольной концентрацией пропорциональна Воспользуемся подстановкой Больцмана. Сначала выразим соответствующие производные через
Подставим (1.253)-(1.265) в (1.22) и получим
Уравнение (6) формально можно преобразовать к виду
Теперь, чтобы рассчитать
перейти в (1.298) от переменной
Поскольку при c= уравнение (1.31) позволяет легко рассчитать Поэтому
Эту плоскость называют плоскостью Матано. В общем случае она не совпадает с первоначальной границей раздела х=0. Физический смысл уравнения (1.33) таков: начало отсчета в уравнении (1.31) должно быть расположено в образце так, чтобы количество диффундирующего вещества, подходящего с одной стороны к этой плоскости, равнялось количеству вещества, уходящего от нее с другой стороны. Метод Больцмана графический, и вычисление Из уравнения (1.31) следует, что
х в уравнении (1.34) отсчитывается от плоскости Матано, расположенной так, чтобы площади под кривой с(х) слева и справа от этой плоскости были равны.
Метод Матано по существу является графическим, и ошибка при его применении сильно растет на концах концентрационной кривой вблизи с1 и с2 . Поэтому определение коэффициента диффузии при малой концентрации одного из компонентов методом Матано практически невозможно. Были предложены различные приближенные методы расчета При массовых расчетах целесообразно использовать ЭВМ. При этом экспериментальная кривая по точкам с(х) с интервалом ∆х вносится в память ЭВМ. ∆х определяется необходимой точностью конечного результата. Алгоритм вычислений следующий: весь заданный интервал по х делится пополам и вычисляют площади S1 и S2 . Затем от большей площади вычитается малая часть и разность прибавляется к меньшей. Такая процедура повторяется до тех пор, пока S1 и S2 не станут равными в пределах заданной точности. В результате этой операции определяют положение плоскости Матано (хm ) . Затем для каждого значения х, в котором вычисляют коэффициент диффузии, определяют
Лекция ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ План 1.Классификация методов 2. Методы радиоактивных изотопов. 3. Локальный ренгеноспектральный метод. 4.Рентгенографический метод. 5.Релаксационные методы. 6. Чувствительность методов.
1 При экспериментальном определении коэффициента диффузии обычно анализируют зависимость концентрации диффундирующего вещества от глубины проникновения и времени с (х, t), либо зависимость количества вещества в образце толщиной 1 от времени q (1, t). Менее точные методы связаны с измерением глубины проникновения диффундирующего вещества. Методы получения концентрационных кривых [кривых зависимости с (х)] естественно разделить на прямые, в которых непосредственно измеряется концентрация (на данной глубине или средняя) или количество вещества: весовые, химические, радиохимические, спектральные, рентгеновские и косвенные, в которых о концентрации судят по изменению какого-либо свойства, чаще всего микротвердости, электропроводности, магнитных свойств, периода решетки и т. д. К косвенным следует отнести и металлографические методы определения глубины проникновения при диффузии, основанные на исследовании микроструктуры разных слоев диффузионной зоны, и специфически «полупроводниковые» методы, среди которых наибольшее распространение получил метод р- n-переходов. Чтобы использовать этот метод, надо исследовать диффузию примеси, дающей проводимость противоположного матрице типа, в полупроводник на некоторую глубину, за пределами которой он сохраняет первоначальную проводимость. Для определения глубины залегания перехода пригодно несколько способов. Два из них известны давно - это химическое окрашивание и электрохимическое покрытие, образующееся в результате реакции замещения. Третий является относительно новым и имеет ряд преимуществ. Он заключается в сканировании светового пятна по образцу с измерением фото-эдс. Глубину перехода в интервале 0,5-10 мкм определяют этим методом с точностью +2 % от средней глубины. Для измерения образцы сошлифовывают под углом
2 Среди прямых методов получения концентрационных кривых наибольшее распространение получили методы, связанные с использованием радиоактивных изотопов, и метод локального рентгеноспектрального анализа - электронного зонда. Радиоактивные изотопы сыграли выдающуюся роль в экспериментальном изучении диффузии, Хотя впервые они были использованы еще в двадцатых годах, однако по настоящему широко метод «меченых» атомов стали применять для исследования диффузии в конце сороковых, начале пятидесятых годов нашего века. Методы, в которых используют радиоактивные изотопы, можно разделить на три группы. К первой группе методовотносятся различные варианты снятия слоев. Обычно на образец наносят тонкий слой радиоактивного вещества, так что размер образца намного бальше толщины нанесенного слоя, и после отжига (вещество диффундирует вдоль оси х) последовательно снимают слои, параллельные фронту диффузии. Измеряют активность J (х) снятого слоя и предполагают, что она пропорциональна концентрации. Коэффициент диффузии определяют по зависимости J (х), строя график в координатах lg J от х2. По тангенсу угла наклона получающейся прямой находят D= 1/9,15 tg а. Оценим чувствительность метода – минимальное значение коэффициента диффузии, которое еще можно определить методом снятия слоев. В соответствии с уравнением (19) будем считать, что концентрация (и интенсивность излучения или активность) радиоактивного вещества в первом слое от поверхности (x~0) приблизительно равна q/2 Обычно удается надежно измерить активность слоя, если c/co~ 10-3. Отсюда следует, что Dmіn≥x2/28 t или Dmіn≥0,0 x2/t . Следовательно, Dmіn тем меньше, чем больше время диффузии и чем меньше суммарная величина снятых слоев. Если снять десять слоев по 25 мкм и принять t ~ 100 ч = 3,6. 105 с (обычный порядок величины для времени диффузионного отжига), то Dmіn ~ 10-10 см2/с. Уменьшение толщины одного слоя в десять раз (анодное растворение, прецизионные станки) дает Dmіn ~ 10-12 см2/с. Это и есть оценка чувствительности метода. В принципе по этой же схеме можно оценить чувствительность метода снятия слоев в его химическом варианте. Естественно, однако, что значение Dmіn окажется значительно больше, поскольку чувствительность радиохимических методов значительно выше, чем обычного химического анализа. Метод снятия слоев характеризуется, таким образом, довольно высокой точностью, однако является трудоемким и требует разрушения образца. Ко второй группеметодов относятся различные варианты абсорбционных методик, основанных на том, что с увеличением глубины проникновения радиоактивного изотопа интенсивность его излучения падает из-за роста поглощения самим образцом. Если принять, что слой толщиной х ослабляет излучение в ехр (- d J = k с (х) ехр (- Принимая для с (х) формулу (19) и интегрируя ( ) от нуля до бесконечности, получим J/Jo = ехр ( Измерив J(t) и зная неточно описывает поглощение излучения (которое обычно применяют для этих целей), особенно в случае полихроматического спектра, и в том, что коэффициент поглощения для твердых растворов обычно неизвестен. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 853. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
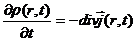 , (1.1)
, (1.1) может быть плотностью любой физической характеристики среды: массы, заряда, числа частиц и т.п. Рассмотрим плотность потока частиц.
может быть плотностью любой физической характеристики среды: массы, заряда, числа частиц и т.п. Рассмотрим плотность потока частиц.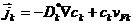 , (1.2 )
, (1.2 ) - коэффициент самодиффузии меченных атомов компонента k;
- коэффициент самодиффузии меченных атомов компонента k; - концентрация компонента k ;
- концентрация компонента k ; 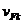 - скорость дрейфа атомов компонента k, обусловленная действием силы F;
- скорость дрейфа атомов компонента k, обусловленная действием силы F;  /с;
/с;  . (1.3 )
. (1.3 ) (1.4 )
(1.4 )
 ,
,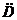 - коэффициент взаимной диффузии.
- коэффициент взаимной диффузии.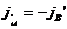 и
и 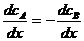 , тогда
, тогда 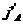 или
или  . Очевидно, что величина
. Очевидно, что величина  , (1.5 )
, (1.5 ) - скорость «течения» решетки.
- скорость «течения» решетки. определяется через поток относительно движущейся системы координат:
определяется через поток относительно движущейся системы координат: . (1.6 )
. (1.6 )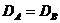 ,то
,то  . Тогда
. Тогда  зависят от состава системы, поэтому их следует относить к определенному составу твердого раствора. Правильно поставленный опыт по взаимной диффузии позволяет определить концентрационную зависимость всех коэффициентов диффузии:
зависят от состава системы, поэтому их следует относить к определенному составу твердого раствора. Правильно поставленный опыт по взаимной диффузии позволяет определить концентрационную зависимость всех коэффициентов диффузии:  для многокомпонентной системы:
для многокомпонентной системы: . ( 1.7 )
. ( 1.7 )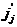 .
. , которые отражают влияние на поток і-того компонента его же градиента концентрации, и перекрестные парциальные коэффициенты диффузии
, которые отражают влияние на поток і-того компонента его же градиента концентрации, и перекрестные парциальные коэффициенты диффузии  , отражающие влияние «чужих» градиентов (
, отражающие влияние «чужих» градиентов (  ). Сравнение (1.6) и (1.7) позволяет установить связь между собственными и парциальными коэффициентами диффузии:
). Сравнение (1.6) и (1.7) позволяет установить связь между собственными и парциальными коэффициентами диффузии: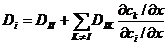 . (1.8 )
. (1.8 ) , и
, и  .
.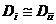 , поэтому часто собственные коэффициенты диффузии мало отличаются от парциальных.
, поэтому часто собственные коэффициенты диффузии мало отличаются от парциальных. . В самом общем случае они не параллельны, так что простая связь
. В самом общем случае они не параллельны, так что простая связь  где D – постоянная величина, несправедлива. В этом случае надо предположить, что каждый компонент потока зависит от всех компонентов градиента. Поэтому уравнения диффузии имеют вид:
где D – постоянная величина, несправедлива. В этом случае надо предположить, что каждый компонент потока зависит от всех компонентов градиента. Поэтому уравнения диффузии имеют вид: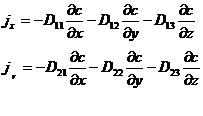 (1.9)
(1.9)  ,
, Тогда первое уравнение из (1.9) даст компоненту потока, параллельную градиенту:
Тогда первое уравнение из (1.9) даст компоненту потока, параллельную градиенту:
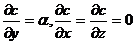 , то компонента , параллельная градиенту, равна:
, то компонента , параллельная градиенту, равна: .
. и ось у
и ось у  неразличимы. Поскольку градиенты концентрации в обоих случаях равны, то из симметрии вытекает, что
неразличимы. Поскольку градиенты концентрации в обоих случаях равны, то из симметрии вытекает, что  , т.е.
, т.е. 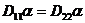 , следовательно
, следовательно  .
. неотличима от оси х, поэтому для кубического кристалла
неотличима от оси х, поэтому для кубического кристалла  .
.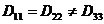 .
. отличаются друг от друга, поэтому
отличаются друг от друга, поэтому 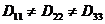 . В гексагональной системе
. В гексагональной системе  с
с  . Однако, если утверждать, что
. Однако, если утверждать, что  является истинным скаляром для любого кубического кристалла, то кроме равенства
является истинным скаляром для любого кубического кристалла, то кроме равенства  Измеряя х-овую компоненту потока, можно определить
Измеряя х-овую компоненту потока, можно определить  :
: . (1.10)
. (1.10) , следовательно,
, следовательно,  (1.11).
(1.11).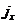 в (1.10) и (1.11) равны или
в (1.10) и (1.11) равны или 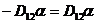 . Это требование симметрии удовлетворяется только при
. Это требование симметрии удовлетворяется только при  . Мы использовали двойную вращательную симметрию, значит
. Мы использовали двойную вращательную симметрию, значит  │ ;
│ ; │;
│; │.
│.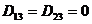 . Поэтому, если концентрация определена методом снятия слоев, то
. Поэтому, если концентрация определена методом снятия слоев, то  можно найти по наклону
можно найти по наклону  , где u – расстояние по нормали от поверхности. Если ось с лежит в плоскости, на которую нанесен изотоп, то поток и градиент опять параллельны и
, где u – расстояние по нормали от поверхности. Если ось с лежит в плоскости, на которую нанесен изотоп, то поток и градиент опять параллельны и  можно найти непосредственно.
можно найти непосредственно.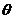 ) с осью с, градиент концентрации составляет угол
) с осью с, градиент концентрации составляет угол  , то
, то .
.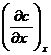 , а через плоскость (x+dx) - DS
, а через плоскость (x+dx) - DS  . В результате за время dt в объеме Sdx остается количество вещества
. В результате за время dt в объеме Sdx остается количество вещества ( 1.12)
( 1.12) получим
получим  если коэффициент диффузии не зависит от координат. Это приведет к увеличению концентрации со временем:
если коэффициент диффузии не зависит от координат. Это приведет к увеличению концентрации со временем: . (1.13 )
. (1.13 ) . (1.14)
. (1.14) .
.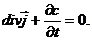 (1.14)
(1.14) .
. )o,t. В частных случаях обе эти величины могут быть постоянными либо равны нулю.
)o,t. В частных случаях обе эти величины могут быть постоянными либо равны нулю. . Так как
. Так как  при всех t>0, то это решение соответствует действию источника, выделяющего количество вещества, пропорциональное
при всех t>0, то это решение соответствует действию источника, выделяющего количество вещества, пропорциональное  , с единицы площади в плоскости х=0в момент времени t=0.
, с единицы площади в плоскости х=0в момент времени t=0.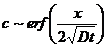 или
или 
 .
. .
.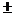 Ах), где В и А - постоянные, как действительное, так и комплексное, удовлетворяет уравнению (1.14).
Ах), где В и А - постоянные, как действительное, так и комплексное, удовлетворяет уравнению (1.14).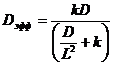 , где L - характерный диффузионный путь, т. е. величина порядка
, где L - характерный диффузионный путь, т. е. величина порядка  .
. <<k и Dэфф≈D. Процесс протекает по диффузионной кинетике и скорость его определяется скоростью диффузии. В этом случае мы имеем дело с граничными условиями типа А, когда задана концентрация на поверхности. Она может быть постоянной либо зависеть от времени. Это - наиболее простой (особенно в случае постоянной концентрации) и достаточно хорошо изученный случай.
<<k и Dэфф≈D. Процесс протекает по диффузионной кинетике и скорость его определяется скоростью диффузии. В этом случае мы имеем дело с граничными условиями типа А, когда задана концентрация на поверхности. Она может быть постоянной либо зависеть от времени. Это - наиболее простой (особенно в случае постоянной концентрации) и достаточно хорошо изученный случай.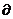 с/
с/  , то они обращаются в условия типа А (диффузионный контроль).
, то они обращаются в условия типа А (диффузионный контроль).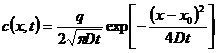 (1.15)
(1.15) . (1.16)
. (1.16) Рис.1 – Концентрационные кривые для диффузии из бесконечно тонкого слоя в полуограниченный образец.
Рис.1 – Концентрационные кривые для диффузии из бесконечно тонкого слоя в полуограниченный образец. . В точке r=0 концентрация убывает по закону t-1.
. В точке r=0 концентрация убывает по закону t-1. . В точке r=0 концентрация убывает по закону t-3/2.
. В точке r=0 концентрация убывает по закону t-3/2. >а с=0, при t=0):
>а с=0, при t=0):
 Рис.2. Концентрационные кривые для полуограниченных образцов
Рис.2. Концентрационные кривые для полуограниченных образцов . (1.18) Концентрационные кривые приведены на рис.2.
. (1.18) Концентрационные кривые приведены на рис.2. (1.19)
(1.19) 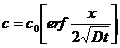 . (1.20)
. (1.20)  . (1.21)
. (1.21) 
 ,
, (1. 23)
(1. 23) , получившую название метода Матано, а вся процедура решения уравнения (1.22) и нахождения концентрационной зависимости
, получившую название метода Матано, а вся процедура решения уравнения (1.22) и нахождения концентрационной зависимости  и является единственным.
и является единственным. ; справа –
; справа – , т.е. при -
, т.е. при - 
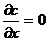 в любой момент времени.
в любой момент времени. Больцман и ввел новую переменную
Больцман и ввел новую переменную 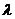 :
:

 (1.24)
(1.24)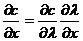 ;
;  ;
;  (1.25)
(1.25)
 (1.26)
(1.26) (1.27)
(1.27) (1.28)
(1.28)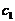 до с:
до с: (1.29)
(1.29) ,
,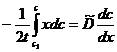 /c -
/c -  /
/  ./с (1.31)
./с (1.31) . Воспользуемся тем, что
. Воспользуемся тем, что 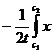 dc = 0 (1.32) – условие выбора «начала отсчета» - точки х=0. (1.32) определяет плоскость начала отсчета. Из (1.32) следует, что существует плоскость х=хm , такая, что
dc = 0 (1.32) – условие выбора «начала отсчета» - точки х=0. (1.32) определяет плоскость начала отсчета. Из (1.32) следует, что существует плоскость х=хm , такая, что . (1.33)
. (1.33) , (1.34)
, (1.34)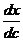 получают, проведя касательную к концентрационной кривой в точке с, тангенс угла наклона которой равен
получают, проведя касательную к концентрационной кривой в точке с, тангенс угла наклона которой равен  определяется как площадь, заключенная между отрезком концентрационной кривой и осями х и с. Знак «-« не должен смущать; очевидно, что
определяется как площадь, заключенная между отрезком концентрационной кривой и осями х и с. Знак «-« не должен смущать; очевидно, что  и по формуле трапеции вычисляют
и по формуле трапеции вычисляют 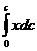 . Полученные значения перемножают, а результат умножают на
. Полученные значения перемножают, а результат умножают на 
 .
. , обычно равным 1° при глубине перехода, большей 1 мкм, и 30' при глубине, меньшей 1 мкм. Диаметр светового пятна изменяется от 2 до 10 мкм.
, обычно равным 1° при глубине перехода, большей 1 мкм, и 30' при глубине, меньшей 1 мкм. Диаметр светового пятна изменяется от 2 до 10 мкм. , а в слое на глубине х составляет
, а в слое на глубине х составляет  . Таким образом, с(х)/с0≈exp(-x2/4Dt.
. Таким образом, с(х)/с0≈exp(-x2/4Dt. х) раз, где
х) раз, где