
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Honorable commission, je oudraies vous presenter mon travail de fin d’etudes au bacalaureat, qui sappelleConstruction du multiplicateur variationnel pour une équation différentielle aux dérivés partielles du deuxième ordre. 2 Mon travail de fin d’études au bacalauréat est consacré à l’examen de l’existence et de la construction d’une solution des problèmes inverses de calcul des variationnels pour les opérateurs différentiels aux différences. 3 On a N(u) opérateur arbitraire. Il est à étudier son potentiel, en cas de résultat positif il est à trouver la fonctionnelle F(u), dont l’ensemble de points stationnaires coincide avec l’ensemble des solutions du problème N(u) = 0. Si l’opérateur donné n’est pas potentiel, on se propose de considérer le problème de la recherché du multiplicateur variationnel. A la résolution du problème par des méthodes variationnelles on a besoin de construire des fonctionnelles, dont les points critiques convergent aux solutions des équations initiales. L’étude du problème de la construction des fonctionnelles recherché commence par vérifier la réalisation des conditions de potentialité des opérateurs correspondants. Il existe des méhtodes effectifs permettant de vérifier la potentialité des opérateurs correspondants pour les équations différentielles aux dérivés partielles [1]. 4 Selon la definition, l’opérateur N(u) est dit l’opérateur potentiel relativement à la forme bilinéire donnée <∙,∙> sur D(N), s’il existe la fonctionnele 5 On appliqué le théorème ci-dessous pour vérifier le potentiel. 6, 7, 8 9 A conditions de satisfaire aux conditions du théorème la fonctionnele Il est à noter qu’en dehor des solutions approximatives des équations, les principes variationnels ont d'autres conséquences importantes, qui sont examinées d’un maniere détaillée dans le chapitre [1]. 10 Dans le premier cas, on examine l’operateur (7) dans le domaine de definition D(N). En appliquant le critère de la potentialité (8) il est facile de vérifier que l'opérateur N(u) n'est pas potentiel. 11 On se propose de rechercher un multiplicateur variationnel  12 On trouve le multiplicateur variationnel. En utilisant les conditions du Théorème [2], on s’assure de la potentialité de l'opérateur (9). 13 Ainsi, pour l'opérateur (9) spécifié dans le domaine concerné 𝐷 ( Il convient de noter que les résultats obtenus pour les équations différentielles aux dérivés partielles ne sont pas toujours reportés sur les équations différentielles aux dérivés partielles a arguments déviés ce qui est lié le plus souvent au domaine de l'opérateur donné. 14 Dans le second cas on considère l'opérateur à arguments déviés (11). Tout comme dans le premier cas on comprend que l'opérateur (11) n’est pas potentiel. 15 On trouve le multiplicateur variationnel, on obtient l'opérateur de la forme (12) et on trouve la fonctionnelle (13). 16 Ainsi pour l'opérateur (12), correspondant à un domaine donné
17 On a examiné deux cas et on a construit les multiplicateurs variationnels et enfin on a cherché les founctionneles.
Je voudrais bien remercier mon chef de recherche de l’aide et du materriel m’ayant été offert à la préparation de mon travail. Je termine à ce point-là et je remecie vous tous de votre attention.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 141. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , tel que la différentielle de Gâteaux de la fonctionnel
, tel que la différentielle de Gâteaux de la fonctionnel  est présenté à la forme ci-dessous
est présenté à la forme ci-dessous de l’operateur (2) peut être trouvée par la formule (6).
de l’operateur (2) peut être trouvée par la formule (6).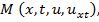 grâce auquel l'opérateur obtenu sera potentiel dans le domaine de definition correspondant D (N), par rapport à une forme bilinéaire donnée (4).
grâce auquel l'opérateur obtenu sera potentiel dans le domaine de definition correspondant D (N), par rapport à une forme bilinéaire donnée (4). ) = 𝐷 (𝑁), qui est potentiel relativement à la forme bilinéaire (4), on a trouvé la fonctionnelle (10), dont l'ensemble des points stationaires coïncide avec l'ensemble des solutions 𝑁 ( 𝑢) = 0.
) = 𝐷 (𝑁), qui est potentiel relativement à la forme bilinéaire (4), on a trouvé la fonctionnelle (10), dont l'ensemble des points stationaires coïncide avec l'ensemble des solutions 𝑁 ( 𝑢) = 0. qui est potentiel par rapport à la forme bilinéaire (4), on trouve la fonctionnelle (13), dont l'ensemble des points fixés coïncide avec l'ensemble de solutions de
qui est potentiel par rapport à la forme bilinéaire (4), on trouve la fonctionnelle (13), dont l'ensemble des points fixés coïncide avec l'ensemble de solutions de 