
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление абсолютной и относительной линейных невязок и их распределение в замкнутом теодолитном ходе. Вычисление координат. ⇐ ПредыдущаяСтр 2 из 2 Линейная невязка- вычисление приращения ∆х и ∆у, содержащие в себе некоторые ошибки и их суммы отличаются от 0 на некоторую величину f Абсолютная линейная невязка: ƒ s= Относительная невязка: ƒ относ.= Вычисление координат: По исправленным приращениям координат вычисляют координаты поворотных точек хода: хn= х n-1 +∆ х испр уn= у n-1 +∆ у испр
18.Прамая и обратная геодезические задачи.Прямая геодезическая задачаВ геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.
Рис. 23. Прямая геодезическая задача Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом. Дано: Точка А( XA, YA ), SAB и αAB. Найти: точку В( XB, YB ). Непосредственно из рисунка имеем: ΔX = XB – XA ; ΔY = YB – YA . Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС: ΔX = SAB · cos αAB ; ΔY = SAB · sin αAB . Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.Знаки приращений координат ΔX и ΔY 
При помощи румба приращения координат вычисляют по формулам: ΔX = SAB · cos rAB ; ΔY = SAB · sin rAB . Знаки приращениям дают в зависимости от названия румба. Вычислив приращения координат, находим искомые координаты другой точки: XB = XA + ΔX ; YB = YA+ ΔY . Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB (рис.24).
Рис. 24. Обратная геодезическая задача Даннная задача решается следующим образом. Сначала находим приращения координат: ΔX = XB – XA ; ΔY = YB – YA . Величину угла rAB определем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB. Для контроля расстояние SAB дважды вычисляют по формулам:
Расстояние SAB можно определить также по формуле
19.Вычисление площади полигона по координатам его вершин. Пусть требуется определить площадь полигона A1, A2, A3, A4, A5 с координатами вершин x1,y1; x2,y2; x3,y3; x4,y4; x5,y5. Площадь полигона S можно представить трапециями, у которых абсциссы являются основаниями, а разности ординат соседних точек высотами S = a1A1A2a2 + a2A2A3a3 + a3A3A4a4 - a5A5A4a4 - a1A1A5a5.
После раскрытия скобок и приведения подобных членов получим 2S = x1y2 - x2y1 + x2y3- x3y2 + x3y4 - x4y3 + x4y5 - x5y4 + x5y1 - x1y5 (2)
После вынесения за скобки x1, x2, x3, x4, x5 будем иметь 2S = x1(y2-y5) + x2(y3-y1) + x3(y4-y2) + x4(y5-y3) + x5(y1-y4) а если из формулы (2) вынести за скобки y1, y2, y3, y4, y5. то будем иметь 2S = y1(x5-x2) + y2(x1-x3) + y3(x2-x4) + y4(x3-x5) + y5(x4-x1). В сокращенном виде эти формулы можно записать так:
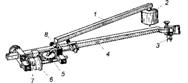
После преобразований получаем формулу в ее нормальном виде. Аналогичное можно проделать и для любого другого многоугольника. 20.Планиметр.Определение площади. Аналитический способ. Если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле: где i - номера вершин многоугольника, пронумерованных по ходу часовой стрелки. По этой же формуле можно вычислить площадь с криволинейными границами, если координаты точек границы сняты так часто, что отрезки между точками можно считать прямыми. В последнем случае съём координат выполняют с помощью специального прибора – дигитайзера, а вычисления выполняют на ЭВМ. Графические способы.Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют. Разбиение площади на простые фигуры выполняют также, применяя палетки. Палетка - лист прозрачного материала (восковки, лавсана, пластика), на который нанесена сетка квадратов размером 2×2 мм или система равноотстоящих параллельных линий. Наложив палетку с квадратами на план, подсчитывают число квадратов, уместившихся в измеряемой площади, оценивая дробные части квадратов на краях участка на глаз. Результат подсчёта умножают на площадь одного квадрата. Палеткой с параллельными линиями площадь делится на трапеции, в каждой из которых измеряют длину средней линии. Суммируя площади трапеций, равные произведению длины средней линии на расстояние между линиями, определяют площадь участка. Точность определения площади с помощью палеток - 1/50. Полярный планиметр. Планиметрами называются приборы для измерения площадей. Наиболее распространён полярный планиметр (рис. 4.11). Он состоит из двух рычагов – полюсного 1 и обводного 4, соединяемых шарниром 8. Полюс планиметра (массивный цилиндр 2 с иглой, втыкаемой в бумагу) в процессе измерения площади остается неподвижным. На конце длинного плеча обводного рычага укреплен шпиль 3 (или лупа с маркой в виде креста в ее центре), которым обводят контур измеряемой площади. На коротком плече обводного рычага крепится каретка с мерным колесиком 6, опирающимся на поверхность бумаги, и счетным механизмом. Когда обводной шпиль 3 (или марка) перемещается по линии контура перпендикулярно рычагу, мерное колесико 6 катится по бумаге. При перемещении обводного шпиля по направлению рычага колесико скользит по бумаге, не вращаясь. При перемещении шпиля в иных направлениях происходит и вращение, и скольжение. Суммарное число оборотов колесика, накопленное при обводке шпилем контура, пропорционально площади, ограниченной контуром.
Рис. 4.11. Полярный планиметр Для подсчета числа оборотов вращение колесика передается на циферблат5. По ободу колесика нанесено 100 делений. Отсчеты по шкале обода берут с помощью верньера 7. Отсчет по планиметру (рис. 4.12) состоит из отсчета числа целых оборотов колесика по циферблату (на рисунке – цифра 6), отсчета десятых и сотых долей оборота - по шкале обода против нуля верньера (цифры 4 и 2) и тысячных долей оборота – по номеру штриха верньера, совпадающего со штрихом на шкале обода (цифра 2). Для измерения площади, обводят её контур, делая при этом два отсчёта по планиметру: один n1- до обвода, другой n2 - после. Площадь вычисляют по формуле S = c·(n2 - n1) , (4.3) где c – цена деления планиметра. Для надёжности площадь измеряют 3 - 5 раз и полученные результаты осредняют. Если во время измерений полюс планиметра располагался внутри измеряемой площади, то вместо формулы (4.3) используют формулу S = c·(n2 - n1+ Q) , где Q - постоянная планиметра.
Рис. 4.12. Отсчет по планиметру: 6422. Цена деления планиметра c зависит от длины обводного рычага и регулируется перемещением по нему каретки с мерным колёсиком и счётным механизмом. Перед измерением площади цену деления планиметра определяют. При этом, расположив полюс в стороне, обводят фигуру, площадь S0 которой известна (например, квадрат километровой сетки на карте) и вычисляют цену деления с = S0 /(n2 - n1). Для определения постоянной Q обводят фигуру с известной площадью, поместив полюс внутри этой площади, после чего вычисляют Q = (S0 /c) - (n2 - n1). Точность определения площади планиметром - 1/300. Электронные планиметры. Электронный полярный планиметр устроен подобно механическому, но имеет электронное счетное устройство и жидкокристаллический дисплей. Электронный роликовый планиметр катится на двух высокофрикционных абразивных роликах, измеряющих смещения по направлению качения. Поворотная штанга с курсором, перемещаемым по контуру площади, измеряет смещения в поперечном направлении. Счетное устройство вычисляет площадь и высвечивает ее величину на дисплее. Электронный роликовый планиметр-дигитайзер позволяет, кроме измерения площади, снимать координаты точек и решать некоторые задачи – определение радиуса окружности, длины дуги, площади сегмента и др. Возможна связь с компьютером через стандартный интерфейс. 21.Виды нивелирования ,применяемые в геодезии.Нивелирование – определение превышения м/у точками земной поверхности. В зависимости от применяемых приборов и методов различают нивелирование тригонометрическое, гидростатическое, барометрическое. Геометрическое нивелирование– вид геод. измерений, позволяющий определить превышение м/у точками или их высоты относительно принятой отсчетной поверхности. Основной принцип Г.Н. заключается в том, что визирный луч прибора должен быть горизонтален. Измерение состоит в отсчитывании по рейкам высоты визирного луча над точками, в которых отвесно установлены рейки. Н.Г – из середины, и вперед. Из середины предпочтительнее. Тригонометрическое нивелирование – чтобы получить превышение методом триг. нивелирования, требуется определить значение угла наклона линии визирования к горизонту и расстояние м/у нивелируемыми точками. Угол измеряют с помощью вертикального круга теодолита. А расстояние измеряется непосредственно. Нивелир – геод. прибор, предназначенный для определения превышений. Нивелиры делятся на 3 вида: Глухой н., Лазерный н. и н. С компенсатором. Глухой н.: зрительная труба, уровень и подставка соединены так, что их взаимное положение можно изменить только при помощи исправительных винтов. Лазерный н.: прибор, основанный на использовании лазерного излучения для создания горизонтальной световой линии или плоскости, относительно которой с помощью нивелирной рейки можно определять превышения. Н. с компенсатором: нивелир, в котором линия визирования занимает горизонтальное положение автоматически после предварительной установки оси вращения в отвесное положение по круговому уровню. (нельзя измерять н. вперед т.к. нет высоты прибора) Поверки геодезических приборов имеют целью обнаружить соответствие взаимного расположения осей и плоскостей данного геодезического прибора. Нивелир Н3 широко использовался в инженерно-геодезических работах.У нивелиров с цилиндрическим уровнем (Н3, НВ1, НТ) : Ось круглого уровня должна быть параллельна оси вращения нивелира. Средняя гориз. нить сетки д/б перпендикулярна к оси вращения нивелира, Визирная ось д/б параллельна оси цилиндрического уровня (главное условие). 22.Сущность геометрического нивелирования. Измерение превышений. Рельеф местности - это совокупность неровностей поверхности земли; он является одной из важнейших характеристик местности. Знать рельеф - значит знать отметки всех точек местности. Отметка точки - это численное значение ее высоты над уровенной поверхностью, принятой за начало счета высот. Отметку любой точки местности можно определить по топографической карте, однако, точность такого определения будет невысокой. Отметку точки на местности определяют по превышению этой точки относительно другой точки, отметка которой известна. Процесс измерения превышения одной точки относительно другой называется нивелированием. Начальной точкой счета высот в нашей стране является нуль Кронштадтского футштока (горизонтальная черта на медной пластине, прикрепленной к устою одного из мостов Кронштадта). От этого нуля идут ходы нивелирования, пункты которых имеют отметки в Балтийской системе высот. Затем от этих пунктов с известными отметками прокладывают новые нивелирные ходы и так далее, пока не получится довольно густая сеть, каждая точка которой имеет известную отметку. Эта сеть называется государственной сетью нивелирования; она покрывает всю территорию страны.Отметки всех пунктов нивелирных сетей собраны в списки - "Каталоги высот". Эти списки непрерывно пополняются, издаются новые каталоги по новым нивелирным ходам. Для нахождения отметки любой точки местности в Балтийской системе высот нужно измерить ее превышение относительно какого-либо пункта, отметка которого известна и есть в каталоге. Иногда отметки точек определяют в условной системе высот, если поблизости нет пунктов государственной нивелирной сети. Вследствие того, что измерение превышений выполняют различными приборами и разными способами, различают: - геометрическое нивелирование (нивелирование горизонтальным лучом), - тригонометрическое нивелирование (нивелирование наклонным лучом), - барометрическое нивелирование, - гидростатическое нивелирование и некоторые другие. Геометрическое нивелирование или нивелирование горизонтальным лучом выполняют специальным геодезическим прибором - нивелиром; отличительная особенность нивелира состоит в том,что визирная линия трубы во время работы приводится в горизонтальное положение. Различают два вида геометрического нивелирования: нивелирование из середины и нивелирование вперед. При нивелировании из середины нивелир устанавливают посредине между точками А и В, а на точках А и В ставят рейки с делениями (рис.4.29). При движении от точки A к точке B рейка в точке А называется задней, рейка в точке В - передней. Сначала наводят трубу на заднюю рейку и берут отсчет a, затем наводят трубу на переднюю рейку и берут отсчет b. Превышение точки B относительно точки А получают по формуле: h = a - b. Если a > b, превышение положительное, если a < b -отрицательное. Отметка точки В вычисляется по формуле: Hв = Hа + h
Высота визирного луча над уровнем моря называется горизонтом прибора и обозначается Hг: Hг = HА + a = HВ + b. При нивелировании вперед нивелир устанавливают над точкой А так, чтобы окуляр трубы был на одной отвесной линии с точкой. На точку В ставят рейку. Измеряют высоту нивелира i над точкой А и берут отсчет b по рейке (рис.4.30). Превышение h подсчитывают по формуле: h = i - b. Отметку точки B можно вычислить через превышение по формуле (4.50) или через горизонт прибора: Hв = Hг - b. Если точки А и В находятся на большом расстоянии одна от другой и превышение между ними нельзя измерить с одной установки нивелира, то на линии AB намечают промежуточные точки 1, 2, 3 и т.д. и измеряют превышение по частям (рис.4.31).
На первом участке A-1 берут отсчеты по задней рейке - a1 и по передней - b1. Затем переносят нивелир в середину второго участка, а рейку с точки A переносят в точку 2; берут отсчеты по рейкам: по задней - a2 и по передней - b2. Эти действия повторяют до конца линии AB. Точки, позволяющие связать горизонты прибора на соседних установках нивелира, называются связующими; на этих точках отсчеты берут два раза - сначала по передней рейке, а затем по задней. Превышение на каждой установке нивелира, называемой станцией, вычисляют по формуле (4.49), а превышение между точками A и B будет равно: hAB = 23.Типы нивелирования. Поверка нивелира Н-3. Нивелир- это геодезический прибор, с помощью которого определяют превышение между точками. Нивелиры в зависимости от их конструкции бывают с цилиндрическим уровнем (уровненные нивелиры) и с компенсатором. В первом случае горизонтальность визирного луча определяется с помощью уровня, а во втором с помощью компенсатора. К названию нивелира также могут добавляться буквы К и Л, а перед буквой Н могут стоять цифры, обозначающие номер модели модификации прибора. Например: 2Н-10КЛ означает: вторая модификация нивелира Н10 с компенсатором и лимбом. В настоящее время широко используют нивелиры Н-3, Н-3К, Н-3КЛ, Н-10Л и др. Нивелир Н-3: Основными частями нивелира являются: подставка7 снабжённая подъёмочными винтами8, элевационный винт6, зрительная труба5, цилиндрический уровень4. Наводящий винт3, круглый уровень1, закрепительный винт2.
Основные оси нивелира: ось вращения прибора, визирная ось зрительной трубы. Для наведения прибора на рейки используют закрепительные и наводящие винты. Круглый винт служит для приведения прибора в отвесное положение. Классификация нивелиров: Высокоточные Н-0.5, точные нивелиры Н-3, технические нивелирыН-10Эльвационный винт предназначен для приведения пузырька цилиндрического уровня в ноль пункт. 1. Поверка: ось круглого уровня должна быть параллельна вертикальной оси прибора. 2. Поверка: вертикальный штрих сетки должен быть параллелен вертикальной оси прибора. 3. Поверка (нитяной отвес): главная визирная ось зрительной трубы должна быть параллельна оси цилиндрического уровня. X=(a+b)/2-(Iпра + iпрв)/2=<4 Юстировка: 1. Nпр=a-x 2. Устанавливают правильный отсчёт эливационным винтом. 3. Возвращают пузырёк цилиндрического уровня в ноль пункт, юстировочным винтом. 24.Нивелирные рейки. Нивелирные рейки используют при проведении различных работ, связанных с определением высот точек или превышений между ними. В зависимости от класса и точности выполняемого нивелирования применяются различные типы реек. Нивелирные рейки служат для измерения высот точек, что определяет величину превышения. Нивелирные рейки различают по материалу изготовления: инварные, алюминиевые и деревянные. Корпус большинства деревянных нивелирных реек выполняют в форме бруска длиной 3 – 4 метра из хорошо выдержанного дерева, пропитанного маслом. Лицевую сторону окрашивают светлой краской, и на ней наносят шашечные или штриховые шкалы. Нивелирные рейки изготавливают как цельные, так и складные. В рабочем (вертикальном) положении рейка устанавливается на выступ металлического башмака. Отвесное положение рейке придается при помощи круглого уровня, привинченного к ее боковой грани. Чтобы убедиться в пригодности нивелирной рейки для нивелирования, внешним осмотром устанавливают четкость делений, отсутствие прогиба, исправность уровня и пятки. Нивелирная рейка (рис. 7.8, а) состоит из двух брусков двутаврового сечения, соединенных между собой металлической фурнитурой. Это позволяет складывать рейку для транспортирования. Рейка имеет градуировку на обеих сторонах. Сантиметровые шашки наносят по всей длине рейки с погрешностью 0,5 мм и оцифровывают через 1 дм. Высота подписанных цифр не менее 40 мм. На основной стороне рейки шашки черные на белом фоне, на другой (контрольной) - красные на белом фоне. На каждой стороне рейки три цветные шашки каждого дециметрового интервала, соответствующие участку в 5 см, соединяются вертикальной полосой. Для контроля при отсчетах по двум сторонам рейки начало первого
оцифрованного дециметрового интервала контрольной стороны смещено по отношению к началу первого оцифрованного дециметрового интервала основной стороны. Для удобства и быстроты установки нивелирные рейки иногда снабжают круглыми уровнями и ручками. На торцах нивелирной рейки укрепляют пятки в виде металлических полос толщиной 2 мм. Рейки маркируют так: например тип РН-10П-3000С означает, что это рейка нивелирная, со шкалой деления (разграфкой с 10 мм, подписью цифр "прямо", длиной 3000 мм, складная). Для точных и технических работ выпускают рейки длиной 3 и 4 м. Нивелирные рейки могут применять в разное время года при различных метеорологических условиях. Температурный диапазон работы реек -40... + 50 °С. Отсчеты по рейкам (рис. 7.8, г) производят по средней нити нивелира - по месту, где проекция средней нити пересекает рейку. Сделать отсчет по рейке - это значит определить высоту визирной оси нивелира над нулем (основанием) рейки. Цифры считывают в такой последовательности: сначала меньшую, видимую вблизи средней нити, подпись (сотни миллиметров), потом прибавляют к ней целое число делений, на которое нить сетки отстоит от меньшей подписи в сторону большей (десятки миллиметров), затем наименьший десятимиллиметровый отрезок делят "на глаз" (количество миллиметров). Отсчет записывают в миллиметрах (на рис. 7.8, г он равен 1514. Во время работы рейки устанавливают на деревянные колья, костыли или башмаки. Костыль (рис. 7.8, б) - металлический стержень с заостренным концом с одной стороны и сферической шляпкой с другой. Для забивки костыля в грунт на верхний торец его надевают крышку. Башмак (рис. 7.8, в) - толстая круглая или треугольная металлическая пластина на трех ножках. В середине пластины укреплен стержень со сферической шляпкой, на которую опирают нивелирные рейки. Рейки устанавливают вертикально "на глаз" или с помощью уровня. Если уровня нет, отсчет по рейке берут при покачивании рейки в сторону нивелира и от него. Из всех видимых отсчетов берут наименьший - он соответствует отвесному положению рейки. 25.Понятие о вертикальной планировки территории. Обработка полевых материалов нивелирования по квадратам : уравнение опорного замкнутого хода. Общие сведения: При строительстве складов, поселков, проектирования садов и парков, возникает необходимость преобразовывать естественные поверхности земли в такую поверхность, которая обеспечивала бы благоприятные условия для строительства и эксплуатации объектов, такое преобразование называют вертикальной планировкой территории. При проектировании такой планировки, нужно решить , где и сколько следует срезать или подсыпать грунта. При этом может ставиться условие , что бы весь срезаемый грунт использовался на подсыпку и не предусматривалось устройство отвалов или карьеров. В этом случае необходимо предусмотреть баланс земляных работ близкий к нулю. Отметку точки на местности , определяют по превышению этой точки, относительно другой точки отметка которой известна. Уравнение опорного замкнутого хода для вычисления невязки: fh=∑hn , т.к (Нк-Нн)=0 где∑hn - сумма средних превышений; (Нк-Нн)-теоритическая сумма превышений; Нн-отметка начального репера; Нк-отметка конечного репера. ∑hi испр=О, для замкнутого хода.
26-Понятие вертикальной планировки территории. Обработка полевых материалов нивелирования по квадратам: вычисление отметок вершин квадрата через горизонт прибора. Общие сведения: При строительстве складов, поселков, проектирования садов и парков, возникает необходимость преобразовывать естественные поверхности земли в такую поверхность, которая обеспечивала бы благоприятные условия для строительства и эксплуатации объектов, такое преобразование называют вертикальной планировкой территории. При проектировании такой планировки, нужно решить , где и сколько следует срезать или подсыпать грунта. При этом может ставиться условие , что бы весь срезаемый грунт использовался на подсыпку и не предусматривалось устройство отвалов или карьеров. В этом случае необходимо предусмотреть баланс земляных работ близкий к нулю. Отметку точки на местности , определяют по превышению этой точки, относительно другой точки отметка которой известна. Для того, что бы получить отметки связующих точек необходимо вычислить горизонт прибора. Горизонт прибора – отметка визирного луча, над исходной уровенной поверхностью на каждой станции вычисляют по отметкам двух соседних точек: ГП1=На+аi ГП2=Нi+вi , где Нi и На – отметки точек, аi и вi – отсчеты по черной стороне рейки на задней и передней связующих точках. 27-Понятие вертикальной планировки территории. Обработка полевых материалов нивелирования по квадратам: Составление плана участка местности в горизонтах. Общие сведения: При строительстве складов, поселков, проектирования садов и парков, возникает необходимость преобразовывать естественные поверхности земли в такую поверхность, которая обеспечивала бы благоприятные условия для строительства и эксплуатации объектов, такое преобразование называют вертикальной планировкой территории. При проектировании такой планировки, нужно решить , где и сколько следует срезать или подсыпать грунта. При этом может ставиться условие , что бы весь срезаемый грунт использовался на подсыпку и не предусматривалось устройство отвалов или карьеров. В этом случае необходимо предусмотреть баланс земляных работ близкий к нулю. Отметку точки на местности , определяют по превышению этой точки, относительно другой точки отметка которой известна. Составление плана местности в горизонталях: Для составления топографического плана участка местности на чертежной бумаги в масштабе 1:500 с помощью сетки квадратов. Проводят горизонтали с помощью палетки , через каждые 0,25м . Горизонтали кратные 1м подписывают и утолщяют. 28.Виды топографических съемок. Топографической съемкой называют комплекс полевых и камеральных работ по определению взаимного планово-высотного расположения характерных точек местности, выполняемых с целью получения топографических карт и планов, а также их электронных аналогов — электронных карт (ЭК) и цифровых моделей местности (ЦММ). 29.Сущность тахеометрической съемки. Полевые работы.Тахеометрическая съемка – топографическая съемка, выполняемая с помощью теодолита или тахеометра и дальномерной рейки (вехи с призмой), в результате которой получают план местности с изображением ситуации и рельефа. Тахеометрическая съемка выполняется самостоятельно для создания планов или цифровых моделей небольших участков местности в крупных масштабах (1: 500 – 1: 5000) либо в сочетании с другими видами работ, когда выполнение стереотопографической или мензульной съемок экономически нецелесообразно или технически затруднительно. Ее результаты используют при ведении земельного или городского кадастра, для планировки населенных пунктов, проектирования отводов земель, мелиоративных мероприятий и т.д. Особенно выгодно ее применение для съемки узких полос местности при изысканиях трасс каналов, железных и автомобильных дорог, линий электропередач, трубопроводов и других протяженных линейных объектов. Слово «тахеометрия» в переводе с греческого означает «быстрое измерение». Быстрота измерений при тахеометрической съемке достигается тем, что положение снимаемой точки местности в плане и по высоте определяется одним наведением трубы прибора на рейку, установленную в этой точке. Тахеометрическая съемка выполняется обычно с помощью технических теодолитов или тахеометров. При использовании технических теодолитов сущность тахеометрической съемки сводится к определению пространственных полярных координат точек местности и последующему нанесению этих точек на план. При этом горизонтальный угол B между начальным направлением и направлением на снимаемую точку измеряется с помощью горизонтального круга, вертикальный угол v – вертикального круга теодолита, а расстояние до точки D – дальномером. Таким образом, плановое положение снимаемых точек определяется полярным способом (координатами в, d), а превышения точек – методом тригонометрического нивелирования. Преимущества тахеометрической съемки по сравнению с другими видами топографических съемок заключаются в том, что она может выполняться при неблагоприятных погодных условиях, а камеральные работы могут выполняться другим исполнителем вслед за производством полевых измерений, что позволяет сократить сроки составления плана снимаемой местности. Кроме того, сам процесс съемки может быть автоматизирован путем использования электронных тахеометров, а составление плана или ЦММ – производить на базе ЭВМ и графопостроителей. Основным недостатком тахеометрической съемки является то, что составление плана местности выполняется в камеральных условиях на основании только результатов полевых измерений и зарисовок. При этом нельзя своевременно выявить допущенные промахи путем сличения плана с местностью. Полевые работы при тахеометрической съемке на станции включают следующие действия: - установку прибора над точкой с известными координатами и приведение его в рабочее положение (допускается выполнять центрирование с погрешностью до 3 см, т.е. на порядок грубее, чем при измерении горизонтальных углов); - определение место нуля вертикального круга (п.28); - составление абриса на станции с указание на нем положения реечных точек; - измерение высоты прибора с погрешностью 1-2 см;- ориентирование нуля лимба горизонтального круга на соседнюю точку съемочного обоснования, координаты которой известны; - наблюдение реечных точек при КЛ: определение расстояния от прибора до рейки по дальномеру, снятие отсчетов по горизонтальному и вертикальному кругам при наведении средней горизонтальной нити на определенный отсчет, например Vj = I; - вычисление углов наклона, неполных превышений и высот реечных точек по формулам ν = Л - М0, h'= 0.5 D' sin2ν, Hj= Hст+ h' + I - Vj. Если рельеф местности позволяет брать отсчет по рейке горизонтальным лучом визирования (в этом случае отсчет по ВК должен быть равен М0), то высоты реечных точек Нi= ГП - аi, где ГП - горизонт прибора ГП = Нст+ I; аi - отсчет по рейке горизонтальным лучом визирования. Результаты измерений и вычислений записывают в журнал тахеометрической съемки . При камеральной обработке проверяют журналы тахеометрической съемки и исправляют ошибки вычислений. Затем с помощью тахеографа наносят на план пикетные (реечные) точки по значениям полярных углов и расстояний. Около пикетных точек выписывают их номера и высоты. В соответствии с абрисами рисуют на плане контуры угодий, элементы ситуации и обозначают их условными знаками. Для отображения рельефа проводят горизонтали. 30.Камеральная обработка тахеометрической съемки. Построение плана. При камеральной обработке проверяют журналы тахеометрической съемки и исправляют ошибки вычислений. Затем с помощью тахеографа наносят на план пикетные (реечные) точки по значениям полярных углов и расстояний. Около пикетных точек выписывают их номера и высоты. В соответствии с абрисами рисуют на плане контуры угодий, элементы ситуации и обозначают их условными знаками. Для отображения рельефа проводят горизонтали
31.Сущность буссольной съемки. Деление на градусном кольце оцифрованы(0-90-180-270;0-90-0-90). Градусное кольцо буссоли называется :азимутальным, румбическим. Нанесение деления на азимутальное кольцо буссоли (по ходу часовой стрелки, против хода часовой стрелки). Магнитная стрелка ориентируется (поворотом крышки буссоли ),спец. Винтом, расположенным (внезу,вверху,др.способом). , съёмка небольших по размерам зем. участков с помощью простейшего геодезического инструмента - буссоли , применяется в тех случаях, когда нужно быстро провести работу, не требующую большой точности. Подлежащий Б. с. участок обозначается на местности деревянными колышками, забиваемыми в углах поворота линий. Съёмка начинается с линий, ограничивающих участок, и ведётся в направлении движения часовой стрелки. Выбрав произвольно исходную вершину, над ней устанавливают буссоль так, чтобы центр буссольного кольца пришёлся на одной вертикали с центром колышка, и, приведя плоскость буссольного кольца в горизонтальное положение, наводят диоптры или трубу буссоли на веху, поставленную вертикально в последующей точке участка. Дав успокоиться магнитной стрелке, производят отсчёт и получают азимут или румб (см.)первой линии (рис. 2). Величина отсчёта записывается в журнал Б. с. Затем производят промер 1-й линии мерной лентой, причём отмечают переходы лентой дорог, ручьев, границ угодий и пр. Результаты измерений записывают в журнал и заносят в абрис (см.). По измерении линии буссоль устанавливается на след. точке и производится определение азимута или румба последующей линии, а затем и дл. этой линии. С подобными измерениями обходят все вершины участка до возвращения в начальную точку. Для контроля измерений азимутов или румбов в каждой последующей вершине измеряют обратный азимут или румб предыдущей линии. Обратный азимут должен отличаться от прямого на 180° (α2=α1±180 ); обратный румб отличается от прямого, при той же градусной величине, противоположным названием. Вследствие того что все измерительные действия сопровождаются неизбежными погрешностями, допускают расхождение между прямым и обратным азимутами на 180° ±1/4, а между румбами - на ±1/4°. Измерение обратных азимутов или румбов становится совершенно необходимым, если съёмщик не уверен в отсутствии местных магнитных аномалий. Б. с. можно также произвести любым угломерным инструментом, снабжённым буссолью, напр., теодолитом (см. Теодолитная съёмка).
32.Виды ошибок , возникающие при измерениях. Отклонение результата измерений L от истинного значения Х измеряемой величины: ∆=L-X называются погрешностями. Погрешности могут быть грубыми, систематическими и случайными. Грубые возникают в результате промахов при измерениях и вычислениях. Грубые погр. Недопустимы и должны полностью исключаться путем проведения повторных измерений. Систематические возникают в процессе измерений за счет инструментальных погрешностей мерных приборов. Случайные неизбежно сопутствуют всем измерениям, исключить их нельзя, но можно ослабить за счет дополнительных измерений. 33.Свойства случайных ошибок Теоретические исследования и опыт измерений показывают, что случайные погрешности обладают следующими основными свойствами: - при определенных условиях измерений, случайные погрешности по абсолютной величине не могут превышать известного предела; - малые по абсолютной величине погрешности появляются чаще, чем большие. - положительные погрешности встречаются так же часто, как и отрицательные; - среднее арифметическое из всех случайных погрешностей равноточных измерений одной и той же величины при неограниченном возрастании числа измерений n стремится к нулю, т.е. где [ ] – обозначение суммы. Формула (5.2) выражает свойство компенсации случайных погрешностей. Этим свойством обладает и сумма попарных произведений случайных погрешностей Каждая погрешность в отдельности не может характеризовать точность измерений, поскольку она случайна. Нужна такая оценка, которая характеризует точность в среднем. Общепринятой характеристикой точности является предложенная К.Ф. Гауссом средняя квадратическая погрешность где Δ1, Δ2, …, Δn – случайные погрешности измерений. Достоинством этой характеристики является ее устойчивость, независимость от знаков отдельных погрешностей и усиленное влияние больших погрешностей. Теоретически строгим значением средней квадратической погрешности считают оценку, получаемую по формуле (5.4) при бесконечно большом числе измерений, то есть при n®¥. Такую строгое значение средней квадратической погрешности часто именуют термином стандарт. На практике приходится пользоваться ограниченным числом измерений, отчего оценки, вычисленные по формуле (5.4) вследствие случайного характера погрешностей Δi отличаются от строгой оценки – стандарта. Средняя квадратическая погрешность определения m по формуле (5.4) приближенно равна Формула (5.4) находит применение при исследовании точности геодезических приборов и методов измерений, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины. Но обычно значение измеряемой величины заранее неизвестно. Тогда вместо формулы Гаусса пользуются формулой Бесселя (см. раздел 5.5), определяющей среднюю квадратическую погрешность по отклонениям результатов измерений от среднего. В большинстве случаев погрешности измерений распределены по нормальному закону, установленному Гауссом. Это означает, что в интервал от –m до + m попадает 68,27% результатов повторных измерений одной и той же величины. В интервал от –2 m до +2 m попадает 95,45%, а в интервал от –3 m до +3 m попадает 99,73%. Таким образом, вероятность того, что случайная погрешность превышает 2 m, равна 4,5%, а что она превышает 3 m - лишь 0,27%. Поэтому погрешности, большие 2 m, считают практически невероятными и относят к числу грубых погрешностей, промахов. Величину 2 m называют предельной погрешностью и используют как допуск при отбраковке некачественных результатов измерений. Dпред = 2 m. В ряде случаев за предельно допустимую погрешность принимают величину 3 m. Величины D, m, Dпред, выражаемые в единицах измеряемой величины, называются абсолютными погрешностями. Наряду с абсолютными применяются также и относительные погрешности, представляющие собой отношение абсолютной погрешности к измеряемой величине. Относительную погрешность принято выражать в виде простой дроби с единицей в числителе, например
34.Понятие о равноточных и неравноточных измерениях. Равноточные измерения – такие, при которых 1. Объект измерений (что измеряют) 2. Субъект измерений (кто измеряет) 3. Средство измерений ( чем измеряют - прибор) 4. Метод измерений (как измеряют – способ, методика) 5. Условия измерений (где измеряют- внешняя среда) не изменяются. Неравноточные изм. – изм., выполненные в различных условиях, приборами различной точности, различным числом приемов и т.д. Надежность результата, выраженная числом, называется его весом. Чем надежнее результат, тем больше его вес. Вес связан с точностью результата измерения, к-рая хар-ется средней кв-ской погр-стью. Поэтому вес результата изм-я принимают обратно пропорциональным квадрату средней кв-ской погр-сти. РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. Основные этапы математической обработки ряда многократных независимых равноточных измерений одной величины. Определение наиболее надёжного значения измеряемой величины. Определение средней квадратической ошибки отдельного результата измерений. Определение средней квадратической ошибки наиболее надёжного значения. Построение доверительных интервалов, с заданной вероятностью накрывающих неизвестные точные значения параметров: истинного значения и среднего квадратического отклонения отдельного результата измерений. Порядок обработки ряда равноточных измерений одной величины, выполняемый по определённой схеме со всеми необходимыми контролями вычислений. НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. Понятие о весе. Обратный вес функции коррелированных и некоррелированных аргументов. Основные этапы математической обработки ряда многократных независимых неравноточных измерений одной величины. Определение среднего весового: наиболее надёжного значения измеряемой величины. Определение средней квадратической ошибки измерения с весом, равным единице. Определение средней квадратической ошибки наиболее надёжного значения. Построение доверительных интервалов для истинного значения и среднего квадратического отклонения измерения с весом, равным единице. Порядок обработки, необходимые контроли вычислений. 35-Геодезическое проектирование горизонтальных площадок с заданной проектной отметкой: определение величины рабочей высоты, расстояние до точки нулевых работ, площади фигур, средних рабочих высот и объема земляных работ. Геодезическое проектирование Инженерно-геодезические изыскания в целях составления топографо-геодезических материалов и получения данных о рельефе местности, существующих зданиях, сооружениях и других элементах планировки территории. Виды выполняемых работ: Задняя проектная отметка Но. При этом составляется картограмма работ: Высоты вершин квадратов; Проектная высота горизонта плоскости. Рабочая отметка ,указанная в каждой вершине высоту насыпи и глубину выемки. Линии нулевых работ, т.е границы между насыпью и выемкой Объем земляных работ. Глубина выемки или высота насыпи в каждой вершине квадрата определяется характеризующей ее величиной рабочей отметкой. h раб = Но-Нф Для определения положения линии нулевых работ находят сначала положение точек нулевых работ. Определение расстояния х до точки нулевых работ :
х=h1/(h1+h2)*L
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 470. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||
 ƒх2+ ƒу2
ƒх2+ ƒу2 , где Р- периметр хода
, где Р- периметр хода

 .
.


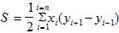
 ,
,



 h =
h = 

 ,
, , (i, j = 1, 2, 3 ... n; i ¹ j).Характеристики точности измерений
, (i, j = 1, 2, 3 ... n; i ¹ j).Характеристики точности измерений ,
, .
. где l - значение измеряемой величины, а N – знаменатель дроби. Относительные погрешности используют, например, когда точность результата измерения зависит от измеряемой величины. Так при одинаковой абсолютной погрешности двух измеренных линий точнее измерена та, длина которой больше.
где l - значение измеряемой величины, а N – знаменатель дроби. Относительные погрешности используют, например, когда точность результата измерения зависит от измеряемой величины. Так при одинаковой абсолютной погрешности двух измеренных линий точнее измерена та, длина которой больше.