
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная сложной функцииЭкономический факультет МАТЕМАТИЧЕСКИЙ АНАЛИЗ методические указания Нижнекамск СОДЕРЖАНИЕ АННОТАЦИЯ................................................................................................. 4
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ.................. 5
КОНТРОЛЬНЫЕ ЗАДАНИЯ......................................................................... 6
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.......................................................... 11
ЛИТЕРАТУРА............................................................................................... 28
Аннотация В пособии представлены задания контрольной работы для студентов заочной формы обучения, рассматриваются основные способы и методы решения задач, необходимые для выполнения контрольного задания. Данное пособие формирует следующие знания, умения и навыки, необходимые для освоения соответствующих компетенций: Знать: символику математического анализа, необходимые на этапах сбора и анализа данных, которые нужны для решения экономических и социально-экономических задач. Уметь: решать типовые задачи по основам раздела курса математического анализа, возникающие на этапе сбора и анализа данных, характеризующих деятельность хозяйствующих субъектов. Владеть: навыками применения аппарата математического анализа для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов. Уметь: применять соответствующие дисциплине методы теоретического исследования для решения экономических задач, проводить расчеты с помощью методов математического анализа. Владеть: методикой применения методов математического анализа для представления и обоснования планов экономической деятельности и результатов работы.  Уметь: осуществлять выбор инструментальных средств математического анализа для обработки экономических данных в соответствии с поставленной задачей. Владеть: навыками применения современного математического инструментария для решения экономических задач. Уметь: применять методы математического анализа и моделирования, теоретического и экспериментального исследования для решения экономических задач, решать дифференциальные уравнения, строить на основе описания ситуаций стандартные экономико-математические модели с использованием понятий предельных и интегральных величин Владеть: методикой построения, анализа и применения моделей математического анализа для оценки состояния и прогноза развития экономических явлений и процессов. Уметь: выполнять операции математического анализа с помощью современных технических средств и информационных технологий. Уметь: педагогически грамотно преподнести учебный материал, компетентно анализировать результаты операции над элементами математического анализа; использовать методологию экономического исследования с помощью элементов математического анализа. Знать: основные понятия математического анализа, позволяющие усовершенствовать учебно-методические разработки. Уметь: применять терминологию и методы математического анализа для оптимизации изложения и решения экономических задач. Владеть: навыками использования символики для изложения экономических материалов. Указания по выполнению контрольной работы 1. Номер варианта контрольной работы соответствует последней цифре номера студенческого билета. 2. В заголовке контрольной работы написать фамилию, имя, отчество, курс, группу, номер студенческого билета, вариант контрольной работы и дату сдачи ее в университет. 3. Решение задач располагать в порядке номеров, указанных в заданиях, сохраняя их номер. 4. Перед решением каждой задачи выписать полностью условие. 5. Решение каждой задачи сопровождать объяснениями и заканчивать ответом. 6. Оформление решений производить аккуратно, с минимальным количеством исправлений. Оставить поля для замечаний проверяющего. 7. Выполненную работу необходимо представить на кафедру Высшей математики не позднее чем за 15 дней до начала сессии.
Контрольные задания № 1. Построить график функции (с помощью преобразования графиков основных элементарных функций). 1. y = 2cos 4. y = sin(x- 7. y = 2½x-1½, 8. y = ½1–x2½, 9. y = 2sinx + 3, 0. y = ln½x-1½.
№ 2. Найти предел функции. 1. а) 2. 3. 4. 5. 6. 7. 8. 9. 0.
№ 3. Вычислить производную функции 1. a) 2. a) 3. a) 4. a) 5. a) 6. a) 7. a) 8. a) 9. a) 0. a)
№ 4. Найти пределы, используя правило Лопиталя 1. 5. 8.
№ 5. Найти наибольшее и наименьшее значения функции на отрезке [–2, 2] и соответствующие значения аргумента. 1. 3. 5. 7. 9.
№ 6. Исследовать функцию и построить ее график. Проверить график в пакете MS Excel 1. 4. 7. 0.
№ 7. Вычислить приближенно, используя дифференциал функции 1. 6. № 8. Найти неопределенные интегралы:
№ 9. Найти определенные интегралы:
10. Найти точки экстремума функции двух переменных: 1. 2.; 3. 4. 5. 6. 7. 8. 9. 0.
№ 11. Найти эмпирическую формулу методом наименьших квадратов в случае линейной зависимости величин. Изобразить на графике исходные значения и прямую линейного тренда. Можно решить данное задание в MS Excel.
Решение типовых примеров 1. Построить график функции у = –4∙sin2x + 1 (с помощью преобразования графиков основных элементарных функций).
у
2) Сжатием графика в 2 раза вдоль оси Ох получаем график функции у=sin2x.
3) Растянем график у = sin2x вдоль оси Оу в 4 раза и получим график функции у = 4sin2x.
у
-4 4) Зеркально отобразив график от оси Ох, получим у = –4sin2x.
у
-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом график функции у = – 4∙sin2x + 1 имеет вид: у
-3
2. Найти Решение. Так как под знаком предела стоит непрерывная в точке х=1 функция, то, используя определение непрерывной функции, имеем:
Ответ. 3. Найти Решение. Функция
Полученная функция определена и непрерывна в точке х=1, поэтому
Ответ: 4. Найти Решение. Здесь требуется найти предел отношения двух бесконечно больших величин. О таком пределе заранее ничего определенного сказать нельзя («неопределенность типа
Ответ: 0.
5. Найти Решение. Такого типа примеры решаются переводом иррациональности из числителя в знаменатель и, наоборот, из знаменателя в числитель. Здесь мы имеем предел разности двух положительных бесконечно больших величин («неопределенность типа [¥–¥]»). От этой неопределенности избавимся, дополнив функцию
Следовательно, Ответ: 0. 6. Найти Решение. Так как Следовательно, Ответ: 7. Найти Решение. Так как х→p, а не к 0, то применить сразу первый замечательный предел нельзя. Поэтому произведем замену переменной:
Ответ: 8. Найти Решение. Выделим у дроби целую часть:
Чтобы использовать второй замечательный предел
Ответ:
9. Найти производную функции: а) у = х + 2; б) y = (2x – 3)(3x + 2); в) у = г) у = ж) Справочный материал Правила дифференцирования: 1) с’ = 0; 2) x’ = 1; 3) (u + v)’ = u’ + v’; 4) (c∙u)’ = c∙u’; 5) (u∙v)’ = u’∙v + u∙v’; 6) (u∙v∙w)’ = u’∙v∙w + u∙v’∙w + u∙v∙w’; 7) Производная сложной функции Если у есть функция от и: у = f(u), где и в свою очередь есть функция от аргумента х: u = φ(x), т.е. если у зависит от х через промежуточный аргумент и, то у называется сложной функцией от х (функцией от функции): y = f(φ(x)). Производная сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной: y’x = y’u u’x Таблица производных:
Решение. а) у = х + 2 Используя правило дифференцирования (3) и формулы (1), (2), имеем: у' = (x + 2)’ = (x)’ + (2)’ = 1 + 0 = 1. б). y = (2x – 3)(3x + 2) y’ = ((2x – 3)(3x + 2))’ = (2x – 3)’∙(3x + 2) + (2x – 3)∙(3x + 2)’ = 2∙(3x + 2) + (2x – 3)∙3 = 12x – 5. Здесь мы использовали правило дифференцирования (5). в) у = Используя правило дифференцирования (7), имеем у’ = г) у = Найдем производную, используя правило дифференцирования (4) и формулу (3). у' = д) у =(x3 – 2x2 + 5)6 Пусть x3 – 2x2 + 5 = и, тогда у = и6. По формуле (3), получим у’ = (и6)’ = 6u5∙u’= 6(x3 – 2x2 + 5)5∙(x3 – 2x2 + 5)’ = 6(x3 – 2x2 + 5)5∙(3x2 – 4x). е) По правилу дифференцирования (7) и формуле (10) получим:
= ж) Используя формулы (4) и (10), имеем:
з) y = tg(3x2 – 1). По формуле (12) имеем: y' = (tg(3x2 – 1))’ = и) По формуле (8), а также (3), (4), (5) имеем:
=
10. Найти предел, используя правило Лопиталя: Решение. Имеем неопределенность вида
Ответ: 1.
11.Найти наибольшее и наименьшее значения функции у = х3 – 12х на отрезке [0, 5]. Решение. Сначала найдем производную функции: у’ = 3х2 – 12. Затем найдем критические точки, т.е. точки, в которых у’ = 0 или не существует: 3х2 – 12 = 0, откуда критические точки х1 = –2, х2 = 2. Точка х1 = –2 не принадлежит отрезку [0, 5], поэтому мы исключаем ее из рассмотрения. Вычислим значения функции в критической точке х2 = 2 и на концах интервала и выберем из них наибольшее и наименьшее: у(2) = – 16, у(0) = 0, у(5) = 65. Ответ: Т.о. наибольшее значение функции на отрезке [0, 5] равно 65, наименьшее равно –16.
12. Исследовать функцию у = Решение. а) Найдем область определения функции. Областью определения этой функции является вся действительная ось, за исключением двух точек х1 = –2 и х2 = 2, в которых имеет место разрыв (знаменатель х2 – 4 = 0). Т.о. область определения: (-∞; -2)U(-2; 2)U(2; +∞) б) Исследуем функцию на четность-нечетность. Функция четная, т.к. у(-х) = в) Найдем вертикальные асимптоты графика функции. Вертикальные асимптоты следует искать в точках разрыва функции или на границе ее области определения. Точками разрыва являются х1 = –2 и х2 = 2. Вычислим пределы функции в окрестностях этих точек. Предел слева Аналогично Следовательно, прямые х = –2 и х = 2 являются вертикальными асимптотами функции. г) Найдем горизонтальные или наклонные асимптоты графика функции. Для этого вычислим пределы: д) Найдем экстремумы и интервалы монотонности. Производная заданной функции у’ =
(0; 2) и (2; +∞) –. убывает y е) Найдем интервалы выпуклости и точки перегиба.
(-2; 2) – выпукла вверх. y ж) Найдем точки пересечения с осями координат. f(0) =
у
1
-2 2 х -1
13. Найти неопределенный интеграл: а) Справочный материал Функция F(x) называется первообразной для функции f(x), если (F(x))’=f(x). Первообразная определена неоднозначно: если F(x) – первообразная для функции f(x), то F(x)+C – также первообразная для данной функции. Множество всех первообразных для функции f(x) называется неопределенным интегралом и обозначается Свойства неопределенного интеграла: 1. 2. 3. Таблица 1 (неопределенных интегралов) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 200. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , 2. y =
, 2. y =  , 3. y = ½cos2x½,
, 3. y = ½cos2x½, ), 5. y = cos½x½, 6. y = sin(x-
), 5. y = cos½x½, 6. y = sin(x-  ) + 1,
) + 1, , б)
, б)  в)
в) 
 , б)
, б)  в)
в) 
 , б)
, б)  в)
в) 
 , б)
, б)  , в)
, в) 
 , б)
, б)  , в)
, в) 
 , б)
, б)  , в)
, в) 
 , б)
, б)  , в)
, в) 
 , б)
, б)  , в)
, в) 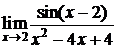
 , б)
, б)  , в)
, в) 
 б)
б)  в)
в) 
 , б)
, б) 
 , , б)
, , б) 
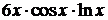 , б)
, б) 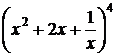
 , , б)
, , б) 
 , б)
, б) 
 , б)
, б) 
 , б)
, б) 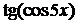
 , б)
, б) 
 , б)
, б) 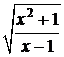
 , б)
, б)  .
. , 2.
, 2.  , 3.
, 3.  , 4.
, 4. 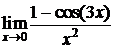 ,
, , 6.
, 6. 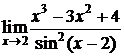 , 7.
, 7.  ,
,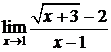 , 9.
, 9.  , 0.
, 0.  .
. 2.
2. 
 4.
4. 
 6.
6. 
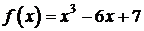 8.
8. 
 0.
0. 
 , 2.
, 2. 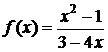 , 3.
, 3.  ,
, , 5.
, 5.  , 6.
, 6.  ,
,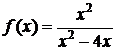 , 8.
, 8.  , 9.
, 9.  ,
, .
. ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ;
; ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 0.
; 0.  .
.







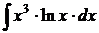






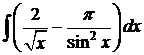














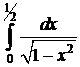















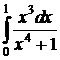













 ;
;
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;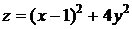 .
. Решение. 1) Сначала построим график функции у = sinx.
Решение. 1) Сначала построим график функции у = sinx.

 1
1


 О х
О х






 4
4















 .
. .
. .
.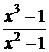 при х=1 не определена («неопределенность типа
при х=1 не определена («неопределенность типа  »), и, следовательно, не является непрерывной в этой точке. Но при всех других значениях х
»), и, следовательно, не является непрерывной в этой точке. Но при всех других значениях х .
. =
=  .
.
 »). Преобразуем функцию под знаком предела, вынося за скобки х в старшей степени, и используем свойства бесконечно малых и бесконечно больших величин. Тогда имеем:
»). Преобразуем функцию под знаком предела, вынося за скобки х в старшей степени, и используем свойства бесконечно малых и бесконечно больших величин. Тогда имеем:
 =
=  =
=  =
=  = 0.
= 0. .
. до разности квадратов:
до разности квадратов: =
=  =
=  .
.
 .
. (первый замечательный предел), то
(первый замечательный предел), то 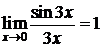 .
.
 .
. .
.
 =
=  =
= 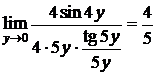 .
. .
. .
. .
. (или
(или  ), обозначим
), обозначим  . Тогда при х→∞ у→0, причем
. Тогда при х→∞ у→0, причем  . Т.о.
. Т.о.
 .
. ;
; д) у =(x3 – 2x2 + 5)6; е)
д) у =(x3 – 2x2 + 5)6; е)  ;
;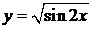 ; з) y = tg(3x2 – 1); и)
; з) y = tg(3x2 – 1); и)  .
. .
.




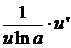
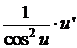


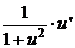
 =
=  .
. .
.
 .
. .
. .
. =
= .
. .
.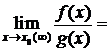
 ), получим:
), получим:
 . Неопределенность вида
. Неопределенность вида  .
. и построить ее график.
и построить ее график. = у(х). Четность функции определяет симметрию ее графика относительно оси Оу.
= у(х). Четность функции определяет симметрию ее графика относительно оси Оу. , предел справа
, предел справа  .
. ,
,  .
. и
и  . Откуда (по формуле y = kx +b) заключаем, что уравнение горизонтальной асимптоты имеет вид: y = 0x +1, т.е. у = 1.
. Откуда (по формуле y = kx +b) заключаем, что уравнение горизонтальной асимптоты имеет вид: y = 0x +1, т.е. у = 1. равна нулю (у’ = 0) при х=0 и не существует при х = ±2. Но критической является только точка х=0 (т.к. значения х = ±2 не входят в область определения функции). Поскольку при x < 0 f’(x) > 0, а при x > 0 f’(x) < 0, то х=0 – точка максимума функции и fmах(x)=
равна нулю (у’ = 0) при х=0 и не существует при х = ±2. Но критической является только точка х=0 (т.к. значения х = ±2 не входят в область определения функции). Поскольку при x < 0 f’(x) > 0, а при x > 0 f’(x) < 0, то х=0 – точка максимума функции и fmах(x)=  = – 1.
= – 1.
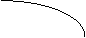 На интервалах (-∞; -2) и (-2; 0) y' + –
На интервалах (-∞; -2) и (-2; 0) y' + –
 функция возрастает
функция возрастает  , на интервалах -2 0 2 x
, на интервалах -2 0 2 x


 Для этого надо найти вторую производную функции у’’ =
Для этого надо найти вторую производную функции у’’ =  . Видно, что уравнение у’’ = 0 не имеет действительных корней, и это исключает существование у графика точек перегиба. Вместе с тем по корням знаменателя (-2 и 2) можно установить, что при переходе через эти значения х знаки у’’ меняются.
. Видно, что уравнение у’’ = 0 не имеет действительных корней, и это исключает существование у графика точек перегиба. Вместе с тем по корням знаменателя (-2 и 2) можно установить, что при переходе через эти значения х знаки у’’ меняются.
 На интервалах (-∞; -2) и (2; +∞) y” + – +
На интервалах (-∞; -2) и (2; +∞) y” + – + функция выпукла вниз, на интервале -2 2 x
функция выпукла вниз, на интервале -2 2 x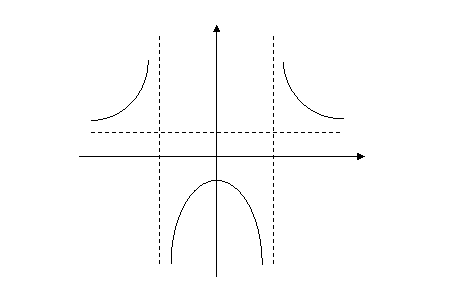 На основании полученных данных построим график заданной функции.
На основании полученных данных построим график заданной функции. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, С – произвольная постоянная (С = const),
, где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, С – произвольная постоянная (С = const),  - знак операции интегрирования, d – знак операции дифференцирования.
- знак операции интегрирования, d – знак операции дифференцирования.
 , где с = const.
, где с = const.
 .
. .
.