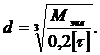Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПЕРЕДАЧИ ТРЕНИЕМ (сцеплением)
ФРИКЦИОННЫЕ ПЕРЕДАЧИ Передают движение за счёт сил трения (лат. frictio – трение). Простейшие передачи состоят из двух цилиндрических или конических роликов - катков.
Передаточное отношение цилиндрической фрикционной передачи определяют как отношение частот вращения или диаметров тел качения.
U = n1/n2=D2/[D1(1-e)], где ε – коэффициент скольжения (0,05 - для передач "всухую"; 0,01 – для передач со смазкой и большими передаточными отношениями). Для конической передачи – вместо диаметров берут углы конусов. Фрикционные передачи выполняются либо с постоянным, либо с регулируемым передаточным отношением (вариаторы). Передачи с постоянным передаточным отношением применяются редко, главным образом, в кинематических цепях приборов, например, магнитофонов и т.п. Они уступают зубчатым передачам в несущей способности. Зато фрикционные вариаторы применяют как в кинематических, так и в силовых передачах для бесступенчатого регулирования скорости. Зубчатые передачи не позволяют такого регулирования.
Достоинства фрикционных передач: + простота тел качения; + равномерность вращения, что удобно для приборов; + возможность плавного регулирования скорости; + отсутствие мёртвого хода при реверсе передачи. Недостатки фрикционных передач: ` потребность в прижимных устройствах; ` большие нагрузки на валы, т.к. необходимо прижатие дисков; ` большие потери на трение; ` повреждение катков при пробуксовке; ` неточность передаточных отношений из-за пробуксовки.  Основными видами поломок фрикционных передач являются: r усталостное выкрашивание (в передачах с жидкостным трением смазки, когда износ сводится к минимуму); r износ (в передачах без смазки); r задир поверхности при пробуксовке.
Поскольку всё это следствие высоких контактных напряжений сжатия, то в качестве проектировочного выполняется расчёт по допускаемым контактным напряжениям [29]. Здесь применяется формула Герца-Беляева, которая, собственно говоря, и была выведена для этого случая. Исходя из допускаемых контактных напряжений, свойств материала и передаваемой мощности определяются диаметры фрикционных колёс
Основные требования к материалам фрикционных колёс: è высокая износостойкость и поверхностная прочность; è высокий коэффициент трения (во избежание больших сил сжатия); è высокий модуль упругости (чтобы площадка контакта, а значит и потери на трение были малы). Наиболее пригодными оказываются шарикоподшипниковые стали типа ШХ15 или 18ХГТ, 18Х2Н4МА. Разработаны специальные фрикционные пластмассы с асбестовым и целлюлозным наполнителем, коэффициент трения которых достигает 0,5. Широко применяется текстолит. Более надёжны передачи, у которых ведущий каток твёрже, чем ведомый, т.к. тогда при пробуксовке не образуются лыски. Применяются обрезиненные катки, однако их коэффициент трения падает с ростом влажности воздуха. Для крупных передач применяют прессованный асбест, прорезиненную ткань и кожу.
РЕМЕННЫЕ ПЕРЕДАЧИ
Ременные передачи применяются для привода агрегатов от электродвигателей малой и средней мощности; для привода от маломощных двигателей внутреннего сгорания. Ремни имеют различные сечения:
б) трапециевидные, клиновые; в) круглого сечения; г) поликлиновые. Наибольшее распространение имеют плоские и клиновые ремни. Плоские ремни применяются как простейшие, с минимальными напряжениями изгиба, а клиновые имеют повышенную тяговую способность. Клиновые ремни применяют по несколько штук, чтобы варьировать нагрузочную способность и несколько повысить надёжность передачи. Кроме того, один толстый ремень, поставленный вместо нескольких тонких будет иметь гораздо большие напряжения изгиба при огибании шкива. В лёгких передачах благодаря закручиванию ремня можно передавать вращение между параллельными, пересекающимися, вращающимися в противоположные стороны валами. Это возможно потому, что жёсткость на кручение ремней вследствие их малой толщины и малого модуля упругости мала. Достоинства ременных передач: + передача движения на средние расстояния; + плавность работы и бесшумность; + возможность работы при высоких оборотах; + дешевизна.
Недостатки ременных передач: ` большие габариты передачи; ` неизбежное проскальзывание ремня; ` высокие нагрузки на валы и опоры из-за натяжения ремня; ` потребность в натяжных устройствах; ` опасность попадания масла на ремень; ` малая долговечность при больших скоростях. Основные критерии расчёта ременных передач: è тяговая способность или прочность сцепления ремня со шкивом; è долговечность ремня. Если не будет выдержано первое условие, ремень начнёт буксовать, если не выполнить второе – ремень быстро разорвётся. Поэтому основным расчётом ременных передач является расчёт по тяговой способности. Расчёт на долговечность выполняется, как проверочный [24,25,29].
Общая длина ремня не зависит от нагрузки [16], следовательно, суммарное натяжение ветвей остаётся постоянным: F1 + F2 = 2Fo. Таким образом, получаем систему двух уравнений c тремя неизвестными:
Эти уравнения устанавливают изменение натяжения ветвей в зависимости от нагрузки Ft, но не показывают нам тяговую способность передачи, которая связана с силой трения между ремнём и шкивом. Такая связь установлена Л.Эйлером с помощью дифференциального анализа.
rF + rfdR – r(F + dF) = 0. Сумма горизонтальных проекций сил: dR – Fsin(dφ/2) – (F+dF)sin(dφ/2) = 0. Отбрасывая члены второго порядка малости и помня, что синус бесконечно малого угла равен самому углу, Эйлер получил простейшее дифференциальное уравнение: dF/F = f dφ. Интегрируя левую часть этого уравнения в пределах от F1 до F2, а правую часть в пределах угла обхвата ремня получаем: F1 = F2 e fα. Теперь стало возможным найти все неизвестные силы в ветвях ремня: F1 = Ft efα /(efα-1); F2 = Ft /(efα-1); Fo = Ft (efα+1)/ 2(efα-1). Полученные формулы устанавливают связь натяжения ремней с передаваемой нагрузкой Ft , коэффициентом трения f и углом обхвата α. Они позволяют вычислить минимальное предварительное натяжение ремня Fo, при котором уже станет возможной передача требуемого вращающего усилия Ft. Нетрудно увидеть, что увеличение f и α улучшает работу передачи. На этом основаны идеи клиноременной передачи (повышается f) и натяжных роликов (повышается α).
При круговом движении ремня на него действует центробежная сила Fv = ρSv2, где S - площадь сечения ремня. Центробежная сила стремится оторвать ремень от шкива и тем самым понижает нагрузочную способность передачи. В ремне действуют следующие напряжения: è предварительное напряжение (от силы натяжения Fo) so = Fo / S; è "полезное" напряжение (от полезной нагрузки Ft) sп = Ft / S; è напряжение изгиба sи = δ Е / D (δ – толщина ремня, Е – модуль упругости ремня, D – диаметр шкива); è напряжения от центробежных сил sv = Fv / S. Наибольшее суммарное напряжение возникает в сечении ремня в месте его набегания на малый шкив smax = so+ sп+sи + sv.
При этом напряжения изгиба не влияют на тяговую способность передачи, однако являются главной причиной усталостного разрушения ремня. Силы натяжения ветвей ремня (кроме центробежных) воспринимаются опорами вала. Равнодействующая нагрузка на опору Fr ≈ 2 Focos(β/2). Обычно эта радиальная нагрузка на опору в 2 … 3 раза больше передаваемой ремнём вращающей силы. Порядок проектного расчёта плоскоременной передачи 1.Выбирают тип ремня. 2.Определяют диаметр малого шкива D1=(110…130)(N/n)1/3, где N–мощность, КВТ, n–частота вращения, об/мин, подбирают ближайший по ГОСТ 17383-73. 3.Выбирают межосевое расстояние, подходящее для конструкции машины 2(D1+D2) ≤a≤15м. 4.Проверяют угол обхвата на малом шкиве: α1=180о-57о(D2-D1)/a, рекомендуется [α1]≥150о, при необходимости на ведомой нити ремня применяют натяжной ролик, который позволяет даже при малых межосевых расстояниях получить угол обхвата более 180о. Угол обхвата можно измерить по вычерченной в масштабе схеме передачи. 5.По передаваемой мощности N и скорости v ремня определяютширину b≥N/(vz[p])иплощадьремня F≥N/(v[k]), где [p] –допускаемая нагрузка на 1мм ширины прокладки, [k]– допускаемая нагрузка на единицу площади сечения ремня. 6.Подбирают требуемый ремень по ГОСТ 101-54; 6982-54; 18679-73; 6982-75; 23831-79; ОСТ 17-969-84. 7.Проверяют ресурс передачи N=3600vzшT. 8.Вычисляют силы, действующие на валы передачи FR= Focos(β/2).
Порядок проектного расчёта клиноременной передачи 1.Выбирают по ГОСТ 1284-68;1284.1-80; 5813-76; РТМ 51015-70 профиль ремня. Большие размеры в таблицах соответствуют тихоходным, а меньшие – быстроходным передачам. 2.Определяют диаметр малого шкива. 3.Выбирают межосевое расстояние, подходящее для конструкции машины 0,55(DM+Dб)+h ≤ a ≤ 2(D1+D2), где h – высота сечения ремня. 4.Находят длину ремня и округляют её до ближайшего стандартного значения. 5.Проверяют частоту пробегов ремня и если она выше допустимой, то увеличивают диаметры шкивов или длину ремня. 6.Окончательно уточняют межосевое расстояние. 7.Определяют угол обхвата на малом шкиве α1 = 180о-57о(D2-D1)/a, рекомендуется [α1] ≥ 120о. 8.По тяговой способности определяют число ремней. 9.При необходимости проверяют ресурс. 10.Вычисляют силы, действующие на валы передачи.
Шкивы плоскоременных передач имеют: обод, несущий ремень, ступицу, сажаемую на вал и спицы или диск, соединяющий обод и ступицу. Шкивы обычно изготавливают чугунными литыми, стальными, сварными или сборными, литыми из лёгких сплавов и пластмасс. Диаметры шкивов определяют из расчёта ременной передачи, а потом округляют до ближайшего значения из ряда R40 (ГОСТ 17383-73*). Ширину шкива выбирают в зависимости от ширины ремня [32]. Во избежание сползания ремня их рабочие поверхности делают выпуклыми. Шероховатость RZ £ 10 мкм.
Чугунные шкивы применяют при скоростях до 30 ÷ 45 м/с. Шкивы малых диаметров до 350 мм имеют сплошные диски, шкивы больших диаметров – ступицы эллиптического переменного сечения. Стальные сварные шкивы применяют при скоростях 60 ÷ 80 м/с. Шкивы из лёгких сплавов перспективны для быстроходных передач до 100м/с.
Плоские ремни должны обеспечивать: è прочность при переменных напряжениях; è износостойкость; è высокое трение со шкивами; è малую изгибную жёсткость. Этим условиям удовлетворяют высококачественная кожа и синтетические материалы (резина), армированные белтинговым тканевым (ГОСТ 6982-54), полимерным (капрон, полиамид С-6, каучук СКН-40, латекс) или металлическим кордом. Применяются прорезиненные тканевые ремни (ГОСТ 101-54), слоистые нарезные ремни с резиновыми прослойками, послойно и спирально завёрнутые ремни. В сырых помещениях и агрессивных средах применяют ремни с резиновыми прокладками [32]. Ремни выпускают конечными и поставляют в рулонах.
Клиноременные шкивы выполняют из тех же материалов, что и плоскоременные. Известны сборные шкивы из стальных тарелок. Быстроходные шкивы требуют балансировки. Материалы клиновых ремней в основном те же, что и для плоских. Выполняются прорезиненные ремни с тканевой обёрткой для большего трения, кордотканевые (многослойный корд) и кордошнуровые ремни (шнур, намотанный по винтовой линии), ремни с несущим слоем из двух канатиков. Иногда для уменьшения изгибных напряжений применяют гофры на внутренней и наружных поверхностях ремня. Клиновые ремни выпускают бесконечными (кольца). Угол клина ремня 40о. Натяжение ремня существенно влияет на долговечность, тяговую способность и к.п.д. передачи. Чем выше предварительное натяжение ремня Fo , тем больше тяговая способность и к.п.д., но меньше долговечность ремня. Натяжение ремня в передачах осуществляется:
®
КОНТРОЛЬНЫЕ ВОПРОСЫ s За счёт каких сил передают движение фрикционные передачи ? s Каковы достоинства и недостатки фрикционных передач ? s Каковы основные виды поломок фрикционных передач ? s Какие материалы применяются для фрикционных передач ? s Какой деталью выделяются ременные передачи среди фрикционных ? s Какие силы действуют в ремне ? s Какие нагрузки действуют на опоры валов колёс ременной передачи ? s Как соединяются концы ремня ? s Какие существуют способы поддержания натяжения ремней ?
ВАЛЫ И ОСИ
Колёса передач установлены на специальных продолговатых деталях круглого сечения. Среди таких деталей различают оси и валы [7,11,38]. Ось – деталь, служащая для удержания колёс и центрирования их вращения. Вал – ось, передающая вращающий момент. Не следует путать понятия "ось колеса", это деталь и "ось вращения", это геометрическая линия центров вращения.
Форма вала определяется распределением изгибающих и крутящих моментов по его длине. Правильно спроектированный вал представляет собой балку равного сопротивления.
Валы и оси вращаются, а следовательно, испытывают знакопеременные нагрузки, напряжения и деформации. Поэтому поломки валов и осей имеют усталостный характер.
Причины поломок валов и осей прослеживаются на всех этапах их "жизни". 1.На стадии проектирования – неверный выбор формы, неверная оценка концентраторов напряжений. 2.На стадии изготовления – надрезы, забоины, вмятины от небрежного обращения. 3.На стадии эксплуатации – неверная регулировка подшипниковых узлов. Для работоспособности вала или оси необходимо обеспечить: è объёмную прочность (способность сопротивляться Mизг и Мкрут); è поверхностную прочность (особенно в местах соединения с другими деталями); è жёсткость на изгиб; è крутильную жёсткость (особенно для длинных валов). Все валы в обязательном порядке рассчитывают на объёмную прочность. Схемы нагружения валов и осей зависят от количества и места установки на них вращающихся деталей и направления действия сил. При сложном нагружении выбирают две ортогональные плоскости (например, фронтальную и горизонтальную) и рассматривают схему в каждой плоскости. Рассчитываются, конечно, не реальные конструкции, а упрощённые расчётные модели, представляющие собой балки на шарнирных опорах, балки с заделкой и даже статически неопределимые задачи [7]. При составлении расчётной схемы валы рассматривают как прямые брусья, лежащие на шарнирных опорах. При выборе типа опоры полагают, что деформации валов малы и, если подшипник допускает хотя бы небольшой наклон или перемещение цапфы, его считают шарнирно-неподвижной или шарнирно-подвижной опорой. Подшипники скольжения или качения, воспринимающие одновременно радиальные и осевые усилия, рассматривают как шарнирно-неподвижные опоры, а подшипники, воспринимающие только радиальные усилия, - как шарнирно-подвижные. Такие задачи хорошо известны студентам из курсов теоретической механики (статики) и сопротивления материалов. Расчёт вала на объёмную прочность выполняют в три этапа.
I. Предварительный расчёт валов Выполняется на стадии проработки Технического Задания, когда известны только вращающие моменты на всех валах машины. При этом считается, что вал испытывает только касательные напряжения кручения tкр = Мвр / Wp £ [t]кр, где Wp - полярный момент сопротивления сечения. Для круглого сечения: Wp = pd3/16, [t]кр= 15 ¸ 20 Н/мм2. Условие прочности по напряжениям кручения удобно решать относительно диаметра вала
Это – минимальный диаметр вала. На всех других участках вала он может быть только больше. Вычисленный минимальный диаметр вала округляется до ближайшего большего из нормального ряда. Этот диаметр является исходным для дальнейшего проектирования.
II. Уточнённый расчёт валов На данном этапе учитывает не только вращающий, но и изгибающие моменты. Выполняется на этапе эскизной компоновки, когда предварительно выбраны подшипники, известна длина всех участков вала, известно положение всех колёс на валу, рассчитаны силы, действующие на вал. Чертятся расчётные схемы вала в двух плоскостях. По известным силам в зубчатых передачах и расстояниям до опор строятся эпюры изгибающих моментов в горизонтальной и фронтальной плоскостях. Затем вычисляется суммарный изгибающий момент
Далее рассчитывается и строится эпюра эквивалентного "изгибающе-вращающего" момента
где α =0,75 или 1 в зависимости от принятой энергетической теории прочности [5], принимаемый большинством авторов равным 1. Вычисляется эквивалентное напряжение от совместного действия изгиба и кручения sэкв = Мэкв / Wp. Уравнение также решается относительно минимального диаметра вала
Или то же самое для сравнения с допускаемыми нормальными напряжениями:
Полученный в уточнённом расчёте минимальный диаметр вала принимается окончательно для дальнейшего проектирования.
III. Расчёт вала на выносливость Выполняется как проверочный на стадии рабочего проектирования, когда практически готов рабочий чертёж вала, т.е. известна его точная форма, размеры и все концентраторы напряжений: шпоночные пазы, кольцевые канавки, сквозные и глухие отверстия, посадки с натягом, галтели (плавные, скруглённые переходы диаметров). При расчёте полагается, что напряжения изгиба изменяются по симметричному циклу, а касательные напряжения кручения – по отнулевому пульсирующему циклу. Проверочный расчёт вала на выносливость по существу сводится к определению фактического коэффициента запаса прочности n, который сравнивается с допускаемым
Здесь ns и nt - коэффициенты запаса по нормальным и касательным напряжениям
где s-1 и τ-1 – пределы выносливости материала вала при изгибе и кручении с симметричным циклом; kσ и kτ – эффективные коэффициенты концентрации напряжений при изгибе и кручении, учитывающие галтели, шпоночные канавки, прессовые посадки и резьбу; εα и ετ – масштабные коэффициенты диаметра вала; sa и τa – амплитудные значения напряжений; sm и τm – средние напряжения цикла (sm= 0, τm=τa); ψσ и ψτ – коэффициенты влияния среднего напряжения цикла на усталостную прочность зависят от типа стали. Вычисление коэффициентов запаса прочности по напряжениям подробно излагалось в курсе "Сопротивление материалов", в разделе "Циклическое напряжённое состояние". Если коэффициент запаса оказывается меньше требуемого, то сопротивление усталости можно существенно повысить, применив поверхностное упрочнение: азотирование, поверхностную закалку токами высокой частоты, дробеструйный наклёп, обкатку роликами и т.д. При этом можно получить увеличение предела выносливости до 50% и более.
КОНТРОЛЬНЫЕ ВОПРОСЫ s Чем различаются валы и оси ? s Какой динамический характер имеют напряжения изгиба в валах и осях ? s Каковы причины поломок валов и осей ? s В каком порядке выполняются этапы прочностного расчёта валов ? s Какой диаметр определяется в проектировочном расчёте валов ?
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 912. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Главное условие работы передачи состоит в том, что момент сил трения между катками должен быть больше передаваемого вращающего момента.
Главное условие работы передачи состоит в том, что момент сил трения между катками должен быть больше передаваемого вращающего момента.
 Являются разновидностью фрикционных передач, где движение передаётся посредством специального кольцевого замкнутого ремня.
Являются разновидностью фрикционных передач, где движение передаётся посредством специального кольцевого замкнутого ремня.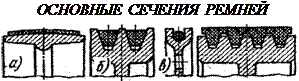 а) плоские, прямоугольного сечения;
а) плоские, прямоугольного сечения; Для создания трения ремень надевают с предварительным натяжением Fo. В покое или на холостом ходу ветви ремня натянуты одинаково. При передаче вращающего момента Т1 натяжения в ветвях перераспределяются: ведущая ветвь натягивается до силы F1, а натяжение ведомой ветви уменьшается до F2. Составляя уравнение равновесия моментов относительно оси вращения имеем –T1 + F1D1/2 – F2D2/2 = 0 или F1 – F2 = Ft, где Ft – окружная сила на шкиве Ft = 2T1/D1.
Для создания трения ремень надевают с предварительным натяжением Fo. В покое или на холостом ходу ветви ремня натянуты одинаково. При передаче вращающего момента Т1 натяжения в ветвях перераспределяются: ведущая ветвь натягивается до силы F1, а натяжение ведомой ветви уменьшается до F2. Составляя уравнение равновесия моментов относительно оси вращения имеем –T1 + F1D1/2 – F2D2/2 = 0 или F1 – F2 = Ft, где Ft – окружная сила на шкиве Ft = 2T1/D1. F1 = Fo + Ft/2;
F1 = Fo + Ft/2; 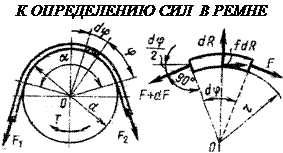 Рассмотрим элементарный участок ремня dφ. Для него dR – нормальная реакция шкива на элемент ремня, fdR – элементарная сила трения. По условию равновесия суммы моментов
Рассмотрим элементарный участок ремня dφ. Для него dR – нормальная реакция шкива на элемент ремня, fdR – элементарная сила трения. По условию равновесия суммы моментов
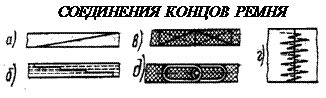 Соединение концов ремней оказывает большое влияние на работу передачи, особенно при больших скоростях. Выбирая тип соединения следует учитывать рекомендации специальной литературы. Самый совершенный способ соединения – склеивание, которое производят для однородных ремней по косому срезу (а), для слоёных по ступенчатой поверхности (б). Надёжным способом считают сшивку встык жильными струнами (в,г). Из механических соединений лучшими являются проволочные спирали, которые продеваются в отверстия и после прессования обжимают концы ремней (д).
Соединение концов ремней оказывает большое влияние на работу передачи, особенно при больших скоростях. Выбирая тип соединения следует учитывать рекомендации специальной литературы. Самый совершенный способ соединения – склеивание, которое производят для однородных ремней по косому срезу (а), для слоёных по ступенчатой поверхности (б). Надёжным способом считают сшивку встык жильными струнами (в,г). Из механических соединений лучшими являются проволочные спирали, которые продеваются в отверстия и после прессования обжимают концы ремней (д). У шкивов клиноременных передач рабочей поверхностью являются боковые стороны клиновых канавок. Диаметр, по которому определяют расчётную длину ремня, называют расчётным диаметром, по ГОСТ 20898-75 он обозначается dp. По этому же ГОСТу для правильного контакта ремня со шкивом угол канавки назначают в зависимости от диаметра шкива.
У шкивов клиноременных передач рабочей поверхностью являются боковые стороны клиновых канавок. Диаметр, по которому определяют расчётную длину ремня, называют расчётным диаметром, по ГОСТ 20898-75 он обозначается dp. По этому же ГОСТу для правильного контакта ремня со шкивом угол канавки назначают в зависимости от диаметра шкива. ®Устройствами периодического действия, где ремень натягивается винтами. Ремень периодически подтягивается по мере вытяжки. Требуется систематическое наблюдение за передачей, иначе возможно буксование и быстрый износ ремня.
®Устройствами периодического действия, где ремень натягивается винтами. Ремень периодически подтягивается по мере вытяжки. Требуется систематическое наблюдение за передачей, иначе возможно буксование и быстрый износ ремня. ®Устройствами постоянного действия, где натяжение создаётся грузом, весом двигателя или пружиной. Часто натяжение происходит за счёт массы двигателя на качающейся плите. К таким устройствам относятся натяжные ролики. Натяжение ремня автоматически поддерживается постоянным.
®Устройствами постоянного действия, где натяжение создаётся грузом, весом двигателя или пружиной. Часто натяжение происходит за счёт массы двигателя на качающейся плите. К таким устройствам относятся натяжные ролики. Натяжение ремня автоматически поддерживается постоянным. Устройствами, автоматически регулирующими натяжение в зависимости от нагрузки с использованием сил и моментов, действующих в передаче. Шкив 1 установлен на качающемся рычаге, который также является осью ведомого колеса зубчатой передачи. Натяжение ремня 2Fo равно окружной силе на шестерне и пропорционально передаваемому моменту.
Устройствами, автоматически регулирующими натяжение в зависимости от нагрузки с использованием сил и моментов, действующих в передаче. Шкив 1 установлен на качающемся рычаге, который также является осью ведомого колеса зубчатой передачи. Натяжение ремня 2Fo равно окружной силе на шестерне и пропорционально передаваемому моменту. Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций. Известны конструкции гибких валов, которые предложил шведский инженер Карл де Лаваль ещё в 1889 г.
Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций. Известны конструкции гибких валов, которые предложил шведский инженер Карл де Лаваль ещё в 1889 г.
 .
.