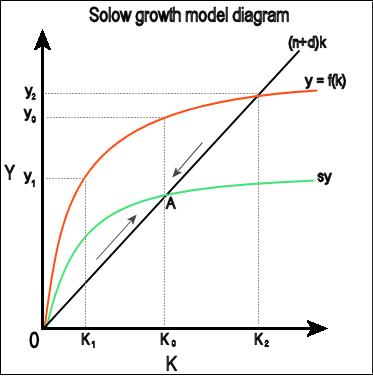
Неоклассическая модель роста Р. Солоу — Т. Свана.

Уравнение сбалансированного роста.Модель устойчивого экономического роста независимо друг от друга предложили в 1956 г. профессор МТИ Роберт Солоу (р. 1924) и профессор Австралийского национального университета в Канберре Тревор Сван(1918 — 1989). Оба они были, также как Харрод и Домар, неокейнсианцами; Сван участвовал в создании Белой книги полной занятости, составленной группой экономистов по заказу правительственного кабинета Лейбористской партии Австралии; Солоу на протяжении десятилетий тесно сотрудничал с П. Самуэльсоном. Но их модель получила название неоклассической,поскольку включила неоклассическую предпосылку гибкости (а не жёсткости) пропорций между применяемыми количественными показателями труда и капитала.

       В статье «Вклад в теорию экономического роста»[97] Р. Солоу доказывал, что при гибкости пропорций труда и капитала и постоянной отдаче от масштаба невозможно противоречие между естественным и гарантированным темпами роста; система может приспособиться к любому темпу роста рабочей силы и в итоге приблизиться к состоянию пропорционального расширения.

       Приняв, как и в модели Харрода—Домара, неизменный темп роста населения и постоянство нормы сбережений s ( откуда I = sY), Солоу включил в свою модель линейно-однородную производственную функцию Y = F{K,L)}, откуда (если разделить все члены уравнения на L и обозначить доход на одного работника Y/L через y, акапиталоинтенсивность K/L через k)  можно получить

 y= L F( k,1) = L f (k).

       Темп прироста k тогда можно записать как

dk / k = d K / K — d L /L = sY/ K — n = s — L / K f (k) — n

или

       dk’ = sf (k) — nk

Это так называемое «фундаментальное уравнение» Солоу словами формулируется следующим образом: прирост капиталовооружённости одного работника — это то, что осталось от удельных инвестиций (сбережений) после того, как удалось обеспечить капитальными благами всех дополнительных работников.

Если sf(k) = nk, то капиталовооруженность остается прежней (dk = 0), т.е. экономика растет без каких-либо изменений в соотношении между факторами. Это и есть сбалансированный рост, траектория которого в модели Солоу, в противоположность модели Харрода—Домара, является устойчивой.

Прямая (n+d)k на графике (рис. 23.2) показывает, сколько каждый работник
должен сберегать и инвестировать из своего дохода, чтобы обеспечить будущих работников (в том числе своих собственных детей) капитальными благами.
Кривая sf(k) демонстрирует, каковы его фактические сбережения
в зависимости от достигнутого уровня капиталовооружённости.
С ростом капиталовооружённости k темп роста инвестиций /сбереже-
ний падает. Вертикальное расстояние между кривой и
прямой обозначает в соответствии с фундаментальным уравнением
Солоу дифференциальное изменение показателя капиталовооружён-
ности dk. В точке k₀ оно равно нулю и наблюдается сбалансирован-
ный рост. Во всех точках левее k₀ (например, k₁) капиталовооружённость
будет расти, а во всех точках правее k₀ (например, k₂) падать,
так что экономика постоянно сдвигается в сторону k_{0 ,} и траектория сбалансированного роста является устойчивой.

В модели Солоу норма сбережений s имеет значение только до выхода экономики на траекторию устойчивого развития: чем больше величина s, тем выше график sk и соответственно уровень k₀. Но как только рост стал сбалансированным, его дальнейший темп зависит только от роста населения и технологического прогресса.

Рис. 23.2. Модель роста Солоу.