
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Анализ подходов по проблеме компромиссовСтр 1 из 2Следующая ⇒ Актуальность данного направления исследований кратко и точно выражена в фундаментальной работе Ю.Б. Гермейера [84] следующим тезисом: «классическая теория игр, во всяком случае, в части теории принятия решений преждевременно и чрезмерно заформализована». Отмечается слабая связь методов бескоалиционной, коалиционной и кооперативной теории игр, которая оказывается необходимой во многих приложениях. Поэтому по-прежнему весьма полезна разработка методов «по информационно-тактическим компромиссам интересов, стратегий и условий, отражающих потребности игровых приложений». При недостаточной систематизации проблеме компромисса в современной теории и практике управления ММС посвящены многочисленные работы. В [54, гл. 6] проанализировано более пятидесяти работ. Придерживаясь по проблеме компромисса предлагаемой в главе классификации от предельного СТЭК (ПСТЭК) до СТЭК-14, в условиях необязательных соглашений и строгой договорной основы можно сформировать представление о важности проблемы и полноте данной классификации. Некоторые условия существования и определения ПСТЭК приводятся в работах [32, 85, 199, 248, 281, 326, 405]. В работе [32] на основе подхода Сталфорда–Кротова рассматриваются условия совпадения Парето–Нэш-решений. Подобного результата можно добиться и подбором параметров ММС [248]. В обзоре [248] приводится работа, в которой рассмотрен случай, когда равновесное решение совпадает с арбитражным, которое, как известно, реализуется на Парето-области. Примыкающему к ПСТЭК понятию кооперативного равновесия, а также его существованию и оценкам посвящена работа [405], причём кооперативное равновесие базируется на угрозе тому, кто отклонился от равновесного кооперативного управления. Данный подход развивается в [326], где в числе других результатов получено: в многошаговой игре кооперативное равновесие достигается, если угрозы состоят из равновесных решений в обратных связях. Определённым образом понятие ПСТЭК и кооперативного равновесия обобщаются в работе [85] как арбитражное равновесие, когда в условиях общих и личных интересов формируются компромиссные показатели, на основе которых определяется Парето-оптимальная ситуация, отступать от которой игрокам невыгодно. Данное понятие пересекается с компромиссами при вступлении в коалицию, о чём пойдёт речь ниже. Таким образом, вопросы ПСТЭК являются актуальными и полезными для приложений.  Идейной базой для создания системной классификации компромиссов в условиях необязательных соглашений являются работы, связанные с улучшением свойств Нэш-равновесия и развитием схем предостережения, например [122, 137, 247, 377, 390], работы, посвященные договорным среднеквадратическим решениям (СКР) и арбитражным схемам (АС), например [32, 39, 84, 120, 168, 190, 226, 247, 248, 325, 345, 365, 381, 396, 429], устойчивым компромиссам при образовании коалиций и коалиционных конфигураций, например [84, 85, 137, 190, 354, 390], коалиционному равновесию [32, 39, 228], некоторым задачам комбинирования кооперативных и некооперативных принципов и другим специфическим задачам [84, 150, 180, 185, 228, 231, 232, 342, 405]. Так, позиционные Нэш-решения являются множеством [122] на области компромиссов, очерченной многогранным конусом с вершиной в точке гарантированных решений и Парето-границей. Поэтому необходим элемент договора для выбора наилучшей точки равновесия: либо на Парето, либо недоминируемой другими решениями [228], либо изменением организационной структуры игры, когда один из игроков получает право первого хода. Улучшение равновесного решения имеет место при изменении условий игры [247]: введении бесконечного интервала времени, позиционных или программных управлений, дискретности информации и др., или при введении специфических форм равновесия [232, 377]: полного равновесия, равновесия повышенного качества с использованием арбитражной схемы Нэша. В работе [137] информационное расширение игры позволяет уравновесить множество исходов первоначальной игры; а обменные стратегии, введённые авторами [390] как побуждение к кооперации, могут порождать дополнительные равновесные решения по Нэшу. Как известно, СКР и АСН являются наиболее известными и алгоритмически простыми компромиссами в договорной ситуации кооперативной игры. Близость Парето-решения к наиболее выгодной всем игрокам «утопической точке» есть очевидный и хорошо изученный договорной компромисс в форме СКР [32, 226, 248, 429]. Также общеизвестны и хорошо изучены свойства арбитражной схемы Нэша (АСН), например [32, 248, 365]. АСН обладает рядом полезных функциональных свойств: оптимальность решений по Парето, симметрия (при равных условиях игроки получают одинаковый выигрыш), инвариантность относительно аффинных преобразований функции выигрыша, независимость относительно несущественных альтернатив (при расширении множества допустимых стратегий арбитражное решение не изменяется). Поэтому АСН используется как компромиссное решение в ММС. Необходимые и достаточные условия существования впервые были получены в работах [325, 365, см. обзор 248] на основе подхода Сталфорда, смотри также необходимые и достаточные условия определения АСН на основе подхода Сталфорда–Кротова [32], достаточные условия продвинуты в [381], интересны первые технические приложения АСН при получении траекторий ракет, направляемых к Юпитеру и Сатурну [248]. Но классическое решение АСН обладает недостатком, состоящим в том, что оно не принимает в расчёт угрозы. В работе [190] производится модификация АСН без ограничения общности в классе биматричной игры (А, В) двух игроков, которая заключается в замене гарантированных значений показателей J* в конструкции АСН на угрозы: В зависимости от потребности анализа рассмотрены и другие модификации АСН. Так, в [39] обсуждается арбитражная схема Райфы, которая приводит в точку Парето, находящуюся на отрезке между гарантированной и утопической точкой, в [345] обсуждается подход Лейтмана в формировании АС, в [396] обсуждаются АС Нэш–Слейтер и Нэш–Слейтер–Гурвиц при решении задач в условиях неопределённости. В [377] АСН используется для анализа полного равновесия и равновесия повышенного качества. Проблема компромисса возникает при образовании коалиций и при обеспечении их устойчивости. Так, в работе [354] получены предпочтительные коалиции в специфической задаче на основе комбинации модифицированной АСН и Нэш-равновесия, а также на основе построения АСН с предостережением. В монографии [137] cреди других вопросов рассматривается вопрос образования коалиции на основе целевого вектора с побочными платежами внутри коалиции, удовлетворяющего специальным условиям достижимости, индивидуальной рациональности, Парето-оптимальности внутри коалиции с арбитражным разрешением по Нэшу. Кроме того, исследуется информационное расширение игры, связанное с обменом информацией в договорном процессе и показано: увеличение взаимной информированности позволяет уравновесить большое число исходов начальной игры; найдены необходимые условия, которым для этого должен удовлетворять исход начальной игры; отмечено ограничение на существование равновесий, указанных в первом пункте, при условии лишь добровольного обмена информацией (см. пример Васина в [137]) и найден обход этих ограничений. Данная работа показывает существенность информационно-такти-ческих компромиссов в реальной задаче. Содержательна последняя работа Ю.Б. Гермейера [85], касающаяся проблемы компромиссов общих и личных интересов с применением арбитражной схемы при формировании чётко и нечётко сформулированных целей коалиции, а также между коалициями при кооперативном объединении равноправных участников. В [342] предложен общий подход представления игры как комбинации некооперативной и кооперативной игры с собственными интересами игроков, при этом полная кооперация достигается на основе договорной максимизации собственных показателей. Вопросы устойчивости образовавшейся коалиционной структуры Р = (K1,…, Km) в игре N игроков с характеристической функцией рассмотрены в монографии [190]. Конфигурация есть пара (Jd, Р) = ( где Конфигурация, удовлетворяющая условию когда никакая Kl не может образоваться, если хотя бы одна из ее подкоалиций может получить больше, чем ей дал дележ, – коалиционно рациональна, а только условию – индивидуально рациональна. Коалиционно-рациональная конфигурация (Jd, P) называется устойчивой, если для каждой угрозы [190] коалиции коалиция Перед тем как перейти к анализу монографий [32, 39, 84, 168], в которых содержатся многочисленные исследования по проблеме компромиссов, рассмотрим некоторые специфические задачи. Так, в работе [231] даны необходимые условия попадания векторного Нэш-равновесия на конкретное подмножество индивидуально-эффективных решений, что является вариацией СТЭК-3 (см. 6.2.2). В работе [150] заявлен компромисс на основе принципов оптимизации по Нэш и Парето для игр в нормальной форме, когда каждый игрок не заинтересован в значительном выигрыше любого из остальных партнёров. В [231, 232] делается попытка объединить седловые точки, равновесие и Парето-оптимальность в рамках единого аппроксимационного понятия экстремальности. Множество компромиссов при исследовании свойств векторной эффективности содержат работы [180]. Примыкающее к коалиционному равновесию понятие доминирования риска Харшаньи, которое будет рассмотрено ниже, дано в работе [228]. В работе [185] на экономическом примере получены следующие результаты по вопросам компромиссов: при увеличении числа взаимодействующих объектов в ММС равновесные и эффективное решения сближаются, а при введении иерархической модели и, следовательно, введении СТЭК ИС за счёт координации можно также обеспечить приближение Нэш-равновесия к Парето-границе. Анализ результатов по компромиссам фундаментальных работ Гермейера [84], Мулена [168], Вайсборда, Жуковского [32] и Вилкаса [39] дан в рефератах данных работ1. Далее кратко комментируются основные результаты анализа. Рассматривая проблему рационального выбора стратегий, автор [84] отмечает стремление к надлежащей взаимной информированности с элементами индивидуализма (самостоятельное «добывание» информации) и коллективизма (добровольный обмен информацией), что является одной из важнейших основ формирования компромиссов, особенно договорных (обязательных соглашений). Рассмотрен вопрос о способах обмена информацией и расширении в связи с этим понятия стратегии. Автор исследует формализованное отношение трех уровней возможного компромисса при образовании коалиции (обмен информацией об игре и обстановке, частичный совместный выбор на основе совместной информации, полное объединение ресурсов и совместный способ действий) и, Так, основная, первая, форма включает свёртку где Ji° – нижняя грань результата, на которую ещё может согласиться игрок, не выходя из коалиции; ri – весовые коэффициенты, и ограничения коалиции где для Xi, имеющих вид gi(x, b) > 0 (x – решения, b – неопределённые факторы), ограничения принимают вид Здесь векторы r и J° – элементы формализации принципа компромисса между интересами игроков. Если игроки не приходят к соглашению относительно ri, они могут обратиться к арбитру и на основе, например АСН, оптимизировать Чтобы подчеркнуть выгоду коллективных действий, автор приводит пример игры с противоположными интересами, в которой вводятся побочные платежи, что приводит к большей эффективности для каждого игрока. При таком перестроении допустимое множество имеет кроме Парето-границы и внутренние точки в отличие от исходной задачи, где Парето-решения составляли всю допустимую область. Анализируя принципы выбора рациональных стратегий [84] с учётом информационных условий, степени конфликтности (коллективизма) и потребностей практики (оптимизация с осреднением, максимин, абсолютно оптимальные стратегии и стратегии наказания, равновесие и т.д.), автор предсказывает важность и актуальность исследований для СТЭК. При этом «прообразом» СТЭК-4 является предложенная при рассмотрении принципа максимина область компромиссов, которой соответствуют все решения с результатами лучшими, чем максиминные. Выводы 1 и 2 второй главы [84] о коллективном обмене информацией при выборе неединственного равновесного решения и коллективности принципа равновесия являются обоснованием для СТЭК-1, 2 (см. стр. 14 реферата [84]). Вывод 3 обосновывает СТЭК-5, а вывод 4 указывает на оригинальный вариант возможного компромисса при образовании коалиции. Подробно анализируя преимущества и недостатки коалиций и рассматривая девять условий образования коалиции, «шесть трудностей» организации коалиций и три условия невозможности коалиций, автор указывает на базовую область возможных коалиций со значениями между минимальными и неулучшаемыми (см. СТЭК-4), а кооперативная игра с характеристической функцией трактуется как вариант договорного арбитража. Определённая ценность в смысле устойчивого компромисса заключается в реализации дополнительных мероприятий, которые способствуют уменьшению опасности сепаратных действий. Среди них следует выделить: одновременность принятия решения, ограничение выбора, переход к коллективным действиям с некоторой устойчивостью к индивидуальным устремлениям (кроме равновесия, УКУ, применяется повторение игры, тогда «обман» вскрывается и может быть предусмотрена процедура наказания), создание органа, следящего за выполнением условий коалиции (переход от СТЭК ММС к СТЭК ИС) и т.д. Для этого в работе рассмотрены подходы и методы решения игр с повторением и иерархические игры. Таким образом, потребное для практики комбинирование классов игр и детальный учёт информационных условий игры в фундаментальной работе [84] является мощным источником для формирования и развития методов исследования на основе СТЭК. Эпиграфом работы Э. Мулена [168] может быть предложена следующая фраза на стр. 12: «противоречие между стабильностью и эффективностью мы считаем главным побудительным мотивом к кооперации…», которая не только выделяет две основные грани игрового результата, но и указывает основную тенденцию развития конфликтной ситуации – кооперативный компромисс. В работе, как отмечалось ранее (гл. 1), впервые вводятся понятия необязательного и обязательного соглашения, которые могут быть важной классификационной основой компромиссов. Напомним, что необязательное соглашение заключается в том, что либо игроки сообща обсуждают, какой исход выбрать, пока не договариваются, либо при достаточной взаимной информации без обсуждения выбирают единственно доминирующее решение, выгодное каждому из них. Эти соглашения не лишают игроков прав отклонения от договорённости и потенциально сохраняют свойства конфликтности. Поэтому после принятия таких соглашений требуется определённая ограниченность обмена информацией между игроками. Если дальнейший обмен и «добывание» информации невозможны, то необязательные соглашения на основе равновесных концепций порождают стабильные компромиссы. Если самостоятельное добывание информации или частичный обмен допустим, то необязательное соглашение может быть сохранено при учёте в процедуре компромисса различных предостережений. (Всё это может служить основой для формирования ряда указанных ранее СТЭК ММС (СТЭК-1, 2, 5 и др.)). Обязательным соглашением является такая договорённость сторон, в результате которой игроки теряют контроль над решениями. После соглашения все проблемы кооперации снимаются, но все они имеют место до соглашения. Теперь значимость стабильности уменьшается, так как нарушения невозможны, можно говорить только о «справедливости», поэтому подход к кооперации при обязательных соглашениях из описательного (какие соглашения являются стабильными при той или иной информационной структуре) становится нормативным (какие соглашения считать справедливыми при заданных соотношениях сил отдельных игроков и коалиций). Потребности практики и тенденция игры позволяют утверждать об определённой взаимосвязи данных видов соглашений и определённой динамике перехода от необязательных соглашений к обязательным, как степени развития игры, что может служить основой формирования СТЭК-4, СТЭК-11, СТЭК-12 и т.д. В работе отмечается, что область между индивидуальными решениями и Парето-границей является минимальной областью переговоров о кооперации (к СТЭК-4), а основой концепции равновесия при предостережениях является a-ядро (прообраз СТЭК-5): множество таких переходов, которые при соответствующих угрозах становятся стабильными относительно отклонений любых коалиций. Рассматриваются a-решения Парето-области, тогда любое a-решение является дележом, в частном случае решения, оптимальные по Парето–Нэш, являются дележом (основа ПСТЭК). Следовательно, a-ядро включает стабильные решения с большей степенью эффективности, чем те, которые обеспечивают необязательные соглашения. Рассмотрены и b- и g-ядра, как a-ядра с дополнительными ограничениями. Установлена прямая связь между осуществимостью стабильности предупреждений и борьбой за лидерство, т.е. переход от СТЭК ММС к СТЭК ИС. Фундаментальная работа Э.М. Вайсборда и В.И. Жуковского [32] систематически раскрывает и формирует новые результаты в четырех основных классах игр (БДИ, КДИ, КОДИ, ИДИ) по трем направлениям: понятие, существование и методы отыскания решений. Определенные идеи и методы касаются проблемы компромиссов. Так, в разделе БДИ рассматриваются вопросы выбора равновесных решений при их неединственности. В разделе КДИ анализируется компромиссная модификация Скеруса решения по Харшаньи на множестве коалиционных структур, когда сформированное множество недоминируемых равновесных решений и значений игры на множестве коалиционных структур используется для формирования характеристической функции В последнем равенстве минимум берется по всем разбиениям Р, (PÌP), содержащим коалицию K, а ur – набор равновесных стратегий, выбранный по методу доминирования Харшаньи из множества всех равновесных стратегий игры Г(P), причем предполагается единственность такого набора в Г(P). Далее, после исследований условий существенности полученной кооперативной игры может быть получен кооперативный дележ. Можно предположить, что подобная комбинация КДИ- и КОДИ-подходов имеет определенную связь с одним из наиболее общих понятий компромиссов – коалиционным равновесием. В том же разделе [32] в рамках предложенного авторами метода поиска УКУ-решений рассматриваются условия получения УКУ–Парето-компромиссов, а в случае отсутствия угрозы (равновесные решения) – получения ПСТЭК. Следует отметить, что эти условия, основанные на подходах Сталфорда–Кротова, достаточно сложны, но позволяют найти решения «в обратных связях». Обсуждаются более простые частные случаи УКУ–Парето-компромисса, когда угроза реализуется среднеквадратической стратегией, а ПСТЭК исследуется для игры с постоянной суммой. В разделе, посвященном КОДИ, отмечается, что применение среднеквадратических решений (СКР), арбитражной схемы Нэша (АСН), С-ядра, Н–М-решения, вектора Шепли и других дележей позволяет сузить множество решений, чтобы все игроки имели результат лучший, чем самостоятельный. Свойствами договорного компромисса обладают принципы, применяемые в КОДИ: договорная устойчивость по Парето, С-ядро, Н–М-решение и оптимальность, явно или неявно предполагающая наличие арбитра (АСН, вектор Шепли). При совместном выборе стратегий формируется показатель оптимальности j (J1,..., JN), который сужает выбор решений на Парето-множестве. Подробно обсуждаются определения и свойства СКР и АСН. Поставлена задача поиска дележа на введенном множестве предпосылок, которые определяются как ПНОК и ПГОК и поэтому подкрепляют важность обсуждаемых в данной главе схем СТЭК. В разделе, посвященном ИДИ, формируется понятие СТЭК ИС и рассматриваются необходимые и достаточные условия его получения как координации центра в виде решения по Штакельбергу. В работе Э.Й. Вилкаса [39] сформировано обобщение основных принципов оптимальности в БДИ, КДИ, КОДИ с позиций введенного автором понятия V-решения и его модификаций, что проектируется на проблему компромиссов. Одним из центральных результатов является формулировка коалиционного равновесия на основе V-решения. Из формулировки следует, что ситуация является коалиционным равновесием, если она принадлежит V-решениям (для которых отсутствуют эффективные угрозы, т.е. угрозы без контругроз) и максимизирует по Парето вектор показателей коалиции. Данная формулировка дополняет трактовку Харшаньи–Скеруса [32], так как при фиксированной коалиционной структуре реализуется лишь Нэш-равновесие, а договорное начало на множестве разбиений достигается на основе кооперативного подхода с использованием характеристических функций. В рамках КОДИ появляется дополнительное качество договорного компромисса в виде устойчивости конфигурации (P, х), где P – разбиение, а х – дележ, и справедливого дележа на основе баланса взаимных требований коалиции. В связи с последним появляется понятие K-ядра, когда конфигурация (P, х) считается устойчивой, если дележ в каждой коалиции Анализ классических решений кооперативной игры в соотношении с Введен и аксиоматически представлен класс критериев Эрроу–Гурвица для обобщенной задачи принятия решения в условиях неопределенности. Как было отмечено ранее, рассмотрено обобщение арбитражного решения Нэша в виде арбитражной схемы Райфы, которая приводит к точке пересечения Парето-области с отрезком, соединяющим гарантированное решение с утопическим. Сформировано понятие пропорционального арбитражного решения, близкое к СТЭК-12, СТЭК-13, которое физически означает постепенное продвижение по лучу, проведенному из точки гарантированных решений к Парето-границе, и, следовательно, дает возможность решать задачу по частям. Исследованы так называемые групповые решения, которые имеют много общего с арбитражными схемами. Групповое решение переплетается с групповыми играми: любое правило типа принятия решения по большинству голосов можно представить в виде просто игры, где основной результат голосования сформулирован как функция общественного блага. 6.2. Компромиссы на основе принципа 6.2.1. Анализ условий для получения предельного СТЭК (ПСТЭК). Общий анализ условий «близости» стабильных Анализ взаимосвязи Парето- и Нэш-решений, а также выявление ситуаций их близости имеет большое значение при исследовании ММС, так как это дает возможность: · оценить эффективность функционирования системы и возможности ее повышения; · выбирать на множестве Парето или в его окрестности точки, обладающие свойством устойчивости к изменению ситуации какой-либо из коалиций, т.е. может рассматриваться как способ уменьшения неопределенности на множестве Парето; · выбирать среди стабильных решений недоминируемые, максимально эффективные; · обеспечить попадание на множество Парето стабильных «угроз-контругроз» (УКУ) и т.д. Эффективность функционирования каждой подсистемы, входящей в многообъектную систему, характеризуется векторным показателем вида
где 1) 2) 3) Отметим, что Соотношение (6.2) означает, что часть компонент векторного показателя системы Таким образом, имеем коалиционную игру вида (6.1), при исследовании которой принципиально возможны варианты: · со скалярными показателями коалиций (когда определены приоритеты внутри коалиций и может быть осуществлена скаляризация каждого вектора · с векторными показателями Случай скалярных показателей коалиции.Предполагаем, что скалярные показатели коалиций могут быть представлены в виде Для простоты обозначений в (6.5) и далее предполагается, что Компоненты То есть в показателях где То есть получили постановку с возмущенной постоянной суммой В показателях Фi более приоритетными являются компоненты, развязанные по вектору параметров. В этом случае векторный показатель Ф обладает свойством: где Показатели Ф1(q) и Ф2(q) развязаны по параметрам q1 и q2 c точностью до функций x1(q) и x2(q) причём значения коэффициентов l11, l13, l21, l23 малы. Возможны смешанные ситуации, например В этом случае трудно выявить какую-либо определённую структуру векторного показателя Ф. Таким образом, учёт особенностей задачи приводит к необходимости проведения дополнительного исследования взаимосвязи Парето- и Нэш- решений для показателей вида (6.6) и (6.7). Наложение на функции x, x1, x2 некоторых условий даёт возможность судить о положении нэшовских точек относительно множества Парето для показателей вида (6.6), (6.7). Утверждение 6.1.Пусть в игре с возмущённой постоянной суммой (6.6) функция x(q) является ограниченной на множестве Q: а q* – произвольное допустимое решение. Тогда на множестве Парето ФП(q), построенном в критериальном пространстве вектора Ф, можно выбрать точку qП такую, что "e > 0 $ h(e) "c £ h(e) úçФ(q*) – Ф(qП)úç£ e. Следствие 6.1. При условиях, сформулированных в утверждении 6.1, решение qr, равновесие по Нэшу относительно векторного показателя Ф (если оно существует) удовлетворяет полученным неравенствам. То есть в критериальном пространстве показателя Ф имеет место близость между нэшовскими и паретовскими точками. Утверждение 6.2.Пусть в игре с векторным показателем (6.7) функции x1(q) x2(q) ограничены на множестве Q: а qr – решение, равновесное по Нэшу относительно показателя Ф и векторов q1 и q2, принадлежащих различным коалициям действия. Тогда существует такое решение qПÎ ФП(q), что "e > 0 $ h(e), "Fi £ h(e), i = 1, 2:úçФ(qr) – Ф(qП)úç £ e. Таким образом, в утверждениях 6.1 и 6.2 обоснована близость Парето- и Нэш-решений для видов взаимодействия подсистем, характеризуемых показателями (6.6) и (6.7). Если приоритеты первичных показателей внутри коалиции распределяются в соответствии с вариантом (6.3), то получаем показатели Фi коалиций достаточно общего вида. При этом решение qr, равновесное по Нэшу, будет, вообще говоря, внутренней точкой множества достижимых внутренних оценок Ф(Q). Случай векторных показателей коалиций.В случае векторных показателей коалиций имеет место векторное равновесие по Нэшу. При этом равновесное решение определяется относительно коалиционной структуры МK = Р. Множество Парето, в этом случае будем иметь в критериальном пространстве первичного векторного показателя JÎ Em. Тот факт, что часть компонент векторного показателя J образует постоянную сумму, можно сформулировать в следующем виде. Существует такое подмножество L Í M = { В [32] показано, что для задачи с постоянной суммой (когда (6.10) справедливо при L = M) любое допустимое решение qÎQ является оптимальным по Парето, и, следовательно, равновесие по Нэшу (если оно существует) обладает свойством оптимальности по Парето. Учёт свойства (6.10) позволяет сформулировать следующее: Утверждение 6.3. Пусть векторный показатель JÎEm обладает на Q свойством (6.10). Тогда множество Q совпадает с множеством QsJ слабо оптимальных по Парето (оптимальных по Слейтеру [224]) решений. Замечание 6.1.Решение q1ÎQsJ, вообще говоря, может не быть оптимальным по Парето, так как множество решений, оптимальных по Парето и оптимальных по Слейтеру, связаны между собой отношением QПJ Í QsJ. (6.11) С учётом условия (6.10) возможна ситуация, когда Следствие 6.2. При условиях, сформулированных в утверждении 6.3, решение qr, равновесное по Нэшу между векторными показателями (6.1) (если оно существует), принадлежит множеству решений, оптимальных по Слейтеру. Отметим, что так же, как и в случае (6.6), условие (6.10) означает, что рассматривается игра с «возмущенной» постоянной суммой где Следовательно, в этом случае можно применить утверждение 6.3 для исследования условий близости Парето- и Нэш-решений. Проведенный анализ показывает, что взаимное расположение Парето- и Нэш-решений в конфликтной ситуации с показателями эффективности вида (1 – 4) определяется свойствами компонент этих показателей, а также соотношением их приоритетов внутри коалиций. Влияние степени конфликтности в ММС с антагонистическим ядром в векторных показателях на свойства СТЭК.Пусть скалярная свёртка показателей i-го объекта: где подвектор qi, например, параметризованного ПКЗУ i-й системы, принадлежит вектору q. Пусть показатели Определение 6.1.Степенью конфликтности (Degree of conflict) в системе (6.14) называется величина Соотношение (6.14) приобретает свойства антагонизма, если любой коалиции из объектов с целевым скаляром Как известно, стабильные решения qr = (q1r,...,qNr) в общем случае при отсутствии ограничений определяются необходимыми условиями оптимальности по Нэшу где qr/qi = (q1r,…, qi-1r, qi, qi+1r,…,qNr). Эффективная Парето-оценка (qП, JП) определяется из экстремальных свойств свёртки где gi определяет значимость (приоритетность) i-го объекта в многообъектной системе. Определение 6.2.Обобщённой степенью конфликтности в системе (6.14) называется величина Для выявления свойств степени конфликтности и анализа области применения ПКЗУ в неантагонистических ситуациях рассмотрим без ограничения общности результата N = 2, li = 2, что в то же время соответствует двухобъектной системе с двухмерными векторными показателями, тогда система (6.13)принимает вид: J1(q) = a J11+(1 – a) J12, J2(q) = b J21+(1 – b) J22. (6.19) Система (6.14)принимает вид J11 + J21 = 0. (6.20) Свёртка (6.17) с учётом (6.20) принимает вид J = gJ1+(1 – g)J2 = agJ11+(1 – g)bJ21+g(1 – a)J12+(1 – g)(1 – b)J22 = = (ag – (1 – g)b)J11+g (1 – a)J12+(1 – g)(1 – b)J22. (6.21) Степень конфликта и обобщённая степень конфликта соответственно: Dc = min[a;b], (6.22) Из (6.22) следует, что степень конфликта по ядру определяется объектом, который имеет меньшую значимость антагонистического ядра (6.20). Из (6.23) следует, что обобщённая степень конфликтности определяется минимальным произведением значимости антагонистического ядра на приоритетность объекта. Далее приведен ряд утверждений, которые раскрывают влияние степени конфликтности на взаимосвязь свойств стабильности и эффективности. Утверждение 6.4.С увеличением степени конфликтности стабильные решения (6.16) сближаются с областью эффективных решений (6.17). Замечание. 6.2. Следует иметь в виду, что по определению допустимые значения множества показателей Jij, j = 1,…, li, i = 1,...,N при наличии связи (6.14) составляют Парето-множество. Но стабильные и эффективные решения рассматриваются на векторе Ji, i = 1,...,N, при этом решения составляют часть границы в векторном пространстве допустимых значений показателей. Утверждение 6.5.При равной приоритетности объектов и равной значимости антагонистического ядра эффективная Парето-оценка формируется и достигается в единственной точке трёхмерной области показателей. Пусть цели объектов равно приоритетны, следовательно, в (6.21) величина g = 0,5. Тогда (6.21) приобретает вид J = (a – b)J11+(1 – a)J12+(1 – b)J22. (6.24) Если a = b ¹ 1, то эффективная Парето-оценка J = (1 – a)(J12+J22)®opt определяется в единственной точке qП. Данная точка является внутренней точкой трёхмерного пространства íJ11(qП), J12(qП), J22(qП)ý. (6.25) Следствие 6.3.Из утверждений 6.4, 6.5 следует, что при увеличении a = b ¹ 1 стабильное решение стремится к найденной точке. Следствие 6.4.При a = b = 1 из выражения (6.24) следует, что оптимизация эффективности вырождается, так как ситуация (6.19), (6.20) становится антагонистической. Утверждение 6.6.При a = b = 1, g ¹ 0,5 оптимизация эффективности (6.21) превращается в оптимизацию показателя объекта, имеющего больший приоритет. Анализируя выражение (6.21), можно обнаружить, что при a = b = 1, g > 0,5; J = (2g – 1)J11, где 2g – 1>0. И наоборот, при g < 0,5; J = (2g – 1)J11 = – (1 – 2g)J11 = (1 – 2g)J21. Утверждение 6.7.Оптимизация (6.21) при a ¹ b при фиксированныхa, b, g даёт точку на Парето-границе трёхмерной допустимой области (J11, J12, J22) или (J21, J12, J22), если обобщённая степень конфликтности (6.23) определяется вторым или первым объектом соответственно. При оптимизации выражения (6.21) процесс Парето-оптимизации будет иметь место, если коэффициенты при показателях находятся в диапазоне (0,1) и их сумма равна единице. Можно показать, что 0 £ g(1 – a) £ 1, 0<(1 – g)(1 – b) £ 1, – 1 £ ga – (1 – g)b £ 1. Тогда: а) если ga ³ (1 – g)b, т.е. б) если ga £ (1 – g)b, т.е. Следовательно, выражение (6.21) имеет место при ag ³ (1 – g)b. При J = ((1 – g)(b – g a)J21+g(1 – a)J12+(1 – g)(1 – b)J22). Утверждение 6.8.Для объекта, который определяет степень конфликтности (6.22), стабильные свойства Нэш-решения менее эффективны. Утверждение 6.9.При различном приоритете объектов (g ¹ 0,5) эффективная оценка на основе (6.21)без компонент антагонистического ядра подчиняется условию: степень значимости антагонистического ядра для объектов обратно пропорциональна приоритетности объекта a / b = (1 – g) / g. (6.26) 6.2.2. СТЭК на основе Парето–Нэш–УКУ–Шепли-комбинаций В данном разделе рассматриваются схемы формирования компромиссов, их систематизация на основе принципа необязательных соглашений и в условиях, в основном, объективной информации о ММС. Технология формирования компромиссов базируется на интерактивных процессах, комбинирующих указанные модули оптимизаций с разной степенью автоматизации интерактивных процедур. Интерактивные процедуры, как и модули оптимизации, реализуются, в основном, в программной системе многокритериальной оптимизации многообъектных динамических систем («МОМДИС»), описание которой дано в работах [48, 213] и главе 9. Результат оптимизации, как и ранее, позволяет получить параметры программно-корректируемых законов управления (ПКЗУ), оптимальные управления и решения в ММС. Параллельная реализация модулей оптимизации позволяет обеспечить реальное время для схем СТЭК. Большинство схем СТЭК полностью реализованы в среде «МОМДИС», «MATLAB», «DELPHI» или в собственной среде, некоторые схемы СТЭК имеют заявочный характер. Далее формируется математическое описание схем СТЭК и общие блок-схемы предлагаемых интерактивных алгоритмов. Выбор наиболее эффективного решения по Нэшу (СТЭК-1).Потребность в данном СТЭК возникает, когда скалярное равновесие по Нэшу при фиксированной структуре ММС является неединственным. Практически речь идет о выборе недоминируемых решений по Нэшу. Определение 6.3.Нэш-решение игры Г(Р) доминирует решение JKi( В рамках СТЭК-1 предполагается, что недоминируемое решение Алгоритмическая схема СТЭК-1 может быть сформирована с помощью одного из методов Парето-оптимизации на конечном множестве точек. Одной из технологически удобных процедур является Парето-оптимизация на основе конусов доминирования, рассмотренная в работах [47, 213, 428, 430] и главе 3. Условие доминирования решения BDJ³ 0, (6.27) где DJ = Знак неравенства меняется, если эффективность заключается в минимизации потерь. Как известно, при В = Е многогранный конус W становится прямоугольным, а процедура оптимизации на основе конуса W сводится к Парето-оптимизации. В терминах рассмотренной ранее реализации данного метода конечное множество значений вектора Jзадаёт таблицу испытаний, по которой происходит попарное сравнение точек таблицы и выделение недоминируемой. При этом на каждой итерации исключаются точки Этап 1. Получение решения, равновесного по Нэшу. Этап 2. Сравнение данного решения с ранее полученными на основе (6.27). Этап 3. Исключение доминируемых решений на данном подмножестве. Данная схема реализуется на интерактивной комбинации программных модулей ПС «MOMДИС». Выбор компромиссного недоминируемого Нэш-решения по критерию уравновешивания потерь в окрестности наилучшего для каждой коалиции Нэш-решения (СТЭК-2). Предыдущий СТЭК-1 может иметь неединственное недоминируемое решение uri, i = 1,2,...,n. Тогда сужение полученного множества может быть достигнуто дополнительными компромиссными условиями близости к наилучшему (идеальному) для каждой коалиции значению показателя По данным двум условиям может быть введён дополнительный критерий оптимизации на конечном множестве недоминируемых Нэш-решений где j, m = 1,...,l; j ¹ m. В (6.29) первая сумма обеспечивает уравновешивание потерь, вторая – близость к идеальной, на основе Нэш-решений, точке, а множитель r(1 ³ r ³ 0) определяет влияние степени близости на компромисс. В частном случае, при l = 3 и r = 0 критерий принимает следующий простой вид:
При достаточно ограниченном числе недоминируемых Нэш-решений после вычисления наборов DiKj остаётся осуществить прямой перебор на конечном множестве для получения компромиссного решения uri. Поэтому общая схема метода для получения СТЭК-2 имеет следующую общую этапную структуру. Этап 1. Получение решения, равновесного по Нэшу. Этап 2. Сравнение данного решения с ранее полученными на основе соотношения (6.27). Этап 3. Исключение доминируемого решения и переход к этапу 1. Этап 4. Нахождение полного набора недоминируемых решений и переход к этапу 5. Этап 5. Получение точек Этап 6. Вычисление разностей Этап 7. Формирование процедуры перебора недоминируемых Нэш-решений по критерию (6.29) при фиксированном r. Интерактивные процедуры Нэш-оптимизации и оптимизации таблицы испытаний Нэш-решений дополняются процедурами вычисления наибольших значений Выбор векторного Нэш-решения относительно идеальной (утопической) для множества допустимых решений точки (СТЭК-3). Как следует из материалов главы 3, раздела 6.1 данной главы и работ [32, 39], коалиционное равновесие при фиксированном разбиении МK = P ММС вырождается в векторное равновесие. Из материалов главы 3, а также из работ [45, 47, 49, 54, 213, 230] следует, что поиск векторного равновесия (векторного Нэш-равновесия и W-равновесия), является достаточно сложной задачей с собственным программным обеспечением. Каждая коалиция теперь имеет векторный показатель, что учитывает элемент субъективности взаимной информации о приоритетности показателей партнёров. Естественно, что скаляризация показателей коалиции с заданными весами приводит к частному случаю векторного Нэш-равновесия: скалярному равновесию по Нэшу. Поэтому при исследовании векторного равновесия по сравнению со скалярным, во-первых, возрастает размерность множества показателей, во-вторых, возрастает число равновесных решений, так как даже при единственности скалярного равновесия перебор вектора весов приводит к множеству решений. Увеличение размерности задачи и расширение множества равновесных решений на множестве допустимых решений приводит к необходимости искать компромиссное решение среди недоминируемых векторных равновесий ( где где UKm – множество параметризованных управлений (решений) коалиции Km, m = 1,...,l. Полученное на основе (6.30), (6.31) решение является наилучшим векторно-равновесным решением для всех коалиций, а поэтому является компромиссным в условиях необязательных соглашений. Общий метод определения компромисса принимает вид следующей многоэтапной последовательности. Этап 1. Получение векторных Нэш-равновесий. Этап 2. Получение множества недоминируемых векторных равновесий. Этап 3. Получение идеального решения на основе критерия (6.31). Этап 4. Получение компромиссного решения на конечном множестве недоминируемых векторных равновесий на основе критерия (6.30). Ввиду сложности решения данной задачи, особенно на первом этапе, данный алгоритм реализован в универсальной программной среде «MATLAB» (глава 3). Надлежащая параметризация программно-корректируемого закона управления и использование параллельной вычислительной среды позволяет реализовать алгоритм в реальном времени. Формирование Парето–Нэш-области компромиссов (ПНОК) (СТЭК-4). Предыдущие СТЭК-1 – СТЭК-3 позволяли получить лучшие решения в рамках одного и того же множества стабильных решений. Данная ПНОК позволяет выделить на области допустимых решений или на области допустимых значений показателей подобласть, где наиболее вероятны следующие шаги по формированию стратегических и нестратегических компромиссов на основе соответственно необязательных соглашений с определённой устойчивостью к отклонениям и строго договорных процедур с обязательными соглашениями и процедурами наказания при невыполнении соглашений, а также определённой «смеси» необязательных и обязательных соглашений. Поэтому, с одной стороны, данная ПНОК является базой для формирования новых компромиссов, с другой стороны, при определенной близости компромиссного значения показателей на основе предыдущих СТЭК к Парето-границе области показателей выделяется малая ОК, каждая точка которой с определённой степенью грубости играет роль собственно СТЭК-4, а в пределе превращается в ПСТЭК. Всё это следует из определения ПНОК на области допустимых значений показателей – свёрток в смысле СТЭК-1 и СТЭК-2 или полного вектора в смысле СТЭК-3. Определение 6.4.ПНОК удовлетворяет системе неравенств: где первое неравенство системы (6.32) имеет смысл многогранного конуса доминирования с матрицей В = Е и вершиной в точке J(uСТЭК-i), а второе имеет смысл семейства лучей, соединяющих точку СТЭК и соответствующее лучу решение uП из подмножества UП Парето-оптимальных решений, также удовлетворяющих первому неравенству. Рисунок 6.1 иллюстрирует данное определение для двухобъектной ММС со скалярными показателями объектов. Метод получения ПНОК базируется на комбинации алгоритмов Парето-оптимизации, Нэш-оптимизации и получения СТЭК-1 (2,3), что может быть представлено в упрощённом виде следующей процедурой. Этап 1. Получение множества скалярных (векторных) недоминируемых Нэш-равновесий. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 224. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
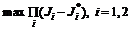 .
.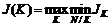
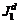 ,...,
,..., 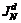 ; K1,…, Kl,..., Km),
; K1,…, Kl,..., Km),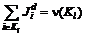 ,
, 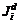 – компонента дележа i-го игрока.
– компонента дележа i-го игрока.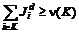 , для
, для 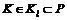 ,
,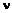 (i), i Î N
(i), i Î N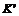 против коалиции
против коалиции 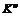
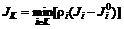 ,
,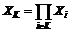 ,
,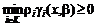 .
.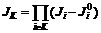 .
.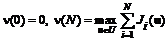 ,
, для всех KÎPÌP.
для всех KÎPÌP.
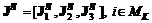 , (6.1)
, (6.1)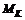 – множество коалиционных индексов разбиения, где компоненты
– множество коалиционных индексов разбиения, где компоненты 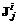 , вообще говоря, сами являются векторными и обладают следующими свойствами:
, вообще говоря, сами являются векторными и обладают следующими свойствами: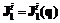 ;
; 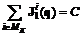 , (6.2)
, (6.2)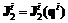 ;
; 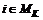 , (6.3)
, (6.3)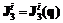 ;
; 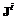 ,
, 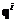 ,
, 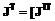 ,...,
,..., 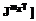 образуют постоянную сумму, т.е. являются существенно конфликтными. Соотношение (6.3) означает, что у каждой коалиции есть показатели, зависящие только от параметров
образуют постоянную сумму, т.е. являются существенно конфликтными. Соотношение (6.3) означает, что у каждой коалиции есть показатели, зависящие только от параметров 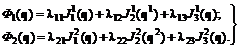 (6.5)
(6.5)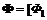 ,
, 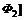 , т.е. число коалиций
, т.е. число коалиций 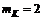 , а компоненты
, а компоненты 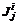 – скаляры.
– скаляры.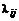 в (6.5) характеризуют значимость первичных показателей внутри коалиций. С точки зрения взаимного расположения Парето- и Неш-решений необходимо проанализировать следующие варианты структуры скалярных показателей Ф1 и Ф2:
в (6.5) характеризуют значимость первичных показателей внутри коалиций. С точки зрения взаимного расположения Парето- и Неш-решений необходимо проанализировать следующие варианты структуры скалярных показателей Ф1 и Ф2: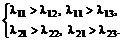
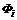 более приоритетными являются компоненты, образующие постоянную сумму. В этом случае векторный показатель
более приоритетными являются компоненты, образующие постоянную сумму. В этом случае векторный показатель 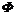 обладает свойством:
обладает свойством: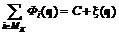 , (6.6)
, (6.6)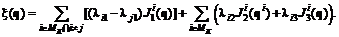
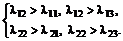
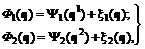 (6.7)
(6.7)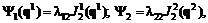
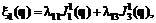
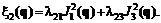
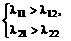 или
или 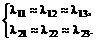
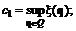
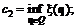 c = c1 – c2, (6.8)
c = c1 – c2, (6.8)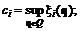
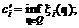 Fi = ci –
Fi = ci – 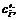 iÎMK, (6.9)
iÎMK, (6.9)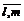 }, что выполняется условие
}, что выполняется условие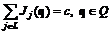 . (6.10)
. (6.10)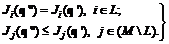
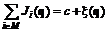 , (6.12)
, (6.12)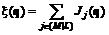 .
.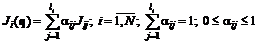 , (6.13)
, (6.13)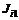 составляют постоянную сумму
составляют постоянную сумму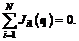 (6.14)
(6.14)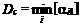 . (6.15)
. (6.15)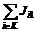 противодействует коалиция из остальных объектов
противодействует коалиция из остальных объектов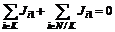 .
.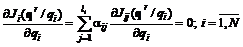 , (6.16)
, (6.16)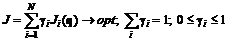 , (6.17)
, (6.17)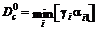 . (6.18)
. (6.18)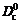 = min[ga;(1 – g)b]. (6.23)
= min[ga;(1 – g)b]. (6.23)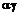 £ (1 – g)b исключается величина J11 и выражение (6.21) принимает вид
£ (1 – g)b исключается величина J11 и выражение (6.21) принимает вид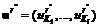 , где Ki ÎP = МK, i = 1,...,l; uÎU
, где Ki ÎP = МK, i = 1,...,l; uÎU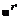 , если
, если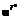 ) ³ JKi(
) ³ JKi( 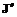 над
над 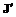 относительно конуса W с матрицей В имеет простой вид
относительно конуса W с матрицей В имеет простой вид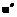 ),
), 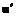 ).
).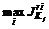 и/или уравновешиванию потерь
и/или уравновешиванию потерь 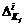 в связи с его недостижимостью, где
в связи с его недостижимостью, где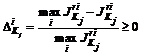 . (6.28)
. (6.28)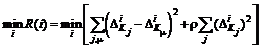 , (6.29)
, (6.29)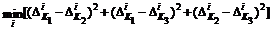 .
.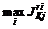 и переход к этапу 6.
и переход к этапу 6.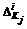 , i = 1,...,n, j = 1,...,l и переход к этапу 7.
, i = 1,...,n, j = 1,...,l и переход к этапу 7.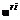 ), наиболее близкое к идеальной точке над множеством допустимых решений по критерию:
), наиболее близкое к идеальной точке над множеством допустимых решений по критерию: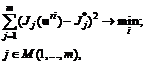 (6.30)
(6.30)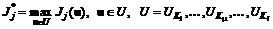 , (6.31)
, (6.31)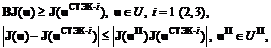 (6.32)
(6.32)