Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Этап 1: выбор начальных приближений УКУ на основе построения ортогональной равномерной сети4.3.1. Формирование ортогональной равномерной сети Рассмотрим скалярные кусочно-непрерывные управления где Управление (4.16а) является параметризованной программой вида (4.14) на r-м интервале ПКЗУ при r = 1 На каждом интервале ПКЗУ формируется (n – r) наборов mK-мерной ортогональной сети шагов управлений (или mK наборов (n – r)-мерной ортогональной сети каждого управления). Тогда для выбора начальных приближений УКУ для ПКЗУ вида (4.16а) для каждого i-го шага управления формируется mK -мерная совместная ортогональная сеть. На областях параметров Множество точек этой сети размерности Если рассматривается двухкоалиционное взаимодействие, то на каждом i-м шаге изменения управления формируется совместная двухмерная ортогональная равномерная сеть, представленная на рис. 4.1.
Рис. 4.1. Формирование ортогональной сети на пространстве параметров В том случае, когда имеет место вырожденное управление, постоянное на всем интервале взаимодействия Густота сети li (длина шага сети) неявно характеризует точность определения области показателей Jв целом, а также области УКУ-равновесных точек в частности. В каждом конкретном случае «густота» достаточная в смысле точности области J определяется свойствами сжатия функционалов J. При этом густота сети и размерность области q непосредственно связаны с временем оптимизации – уменьшение шага сети ведет к значительному увеличению продолжительности работы алгоритма поиска УКУ-оптимальных решений, так как количество «ячеек» сети  где Так как УКУ-решения, полученные на первом этапе алгоритма оптимизации методом УКУ, используются только для формирования начальных приближений для дальнейшей оптимизации, то возможен выбор достаточно большого значения шага (малой густоты) сети l. При этом имеет место увеличение быстродействия алгоритма. Например, для ряда приложений имеет место На втором этапе для рассматриваемых в работе приложений трактовка (4.16) является начальным приближением ПКЗУ многошагового взаимодействия, когда 4.3.2. Алгоритм получения сетевых УКУ-решений Алгоритм вычисления сетевых УКУ-решений является итерационным и в общем случае имеет следующий вид: Шаг 1: задается модель конфликта, определяются параметры системы; Шаг 2: для r-го интервала ПКЗУ формируется ортогональная равномерная сеть c Шаг 3: для точки в сети c координатами Шаг 4: а) если «угроза» существует, проверяется наличие «контругрозы» коалиции N/K, т.е. точки с координатами Шаг 5: а) если «контругроза» существует, то переходим на шаг 6а; Шаг 6: а) точка Шаг 7: а) переходим к следующей точке сети на шаг 3; б) если перебраны все точки сформированной сети, то переходим к шагу 2 для (r+1)-го интервала ПКЗУ. 4.4. Этап 2: оптимизация управления ММС на основе модифицированных достаточных условий локальных УКУ (ЛУКУ) [50] и метода моментов Н.Н. Красовского [129] 4.4.1. Общий вид достаточных условий ЛУКУ Э. Вайсборда В соответствии с общими принципами формирования коалиционной структуры [32] вводится коалиционное разбиение где P – множество коалиционных структур при частичном объединении Kl из P. Показатель потерь коалиции Kl: где Коалиционное динамическое описание системы: Здесь, как и ранее, множество 1) для любого набора уравнений 2) компоненты ni-мерных вектор-функций 3) управление 4) множество где Локальной угрозой коалиции Локальной контругрозой контркоалиции N/K является возможность замены контркоалицией N/K управления Локальный характер угроз и контругроз принят к рассмотрению для уточнения сетевых УКУ в промежутках между узлами сети. Определение 4.5.Локальной угрозой и контругрозой для коалиции K называется набор управлений Определение 4.6.Если один и тот же набор управлений является локальной угрозой и контругрозой для любой допустимой коалиции K, тоu(t) называется локальной угрозой и контругрозой коалиционной игры. Стабильные свойства ЛУКУ обобщают известные свойства равновесия по Нэшу, при которых контругроза реализуется уже для соотношения (4.21) с изменением знака. Для получения достаточных условий класс допустимых вариаций uK(t) и где Постоянные gK,gN/K можно выбрать настолько малыми по абсолютной величине, что при ограниченных Вводятся системы вида где Теорема 4.1 [32]. Для того чтобы а) векторы g1(K) = gK,N/K(t)иg2(K) = gN/K,N/K(t) были линейно независимы (равенство a1×g1(t)+a2×g2(t) = 0 возможно лишь при a1 = a2 = 0), б) для любых допустимых Как и в общем случае, данные достаточные условия локальных УКУ также являются сложными для практических применений. Действительно, для выполнения условия а) существует, в свою очередь, необходимое условие: если g1 и g2 линейно независимы, то определитель Грамма [32] где Во-первых, если это условие выполняется, то функции могут и не быть линейно-независимы, во-вторых, это условие трудно проверяется. Для проверки условия б) необходимо решить интегральное уравнение и убедиться, что кроме тривиального решения И, наконец, необходимо во всех случаях применения иметь точное описание функции перехода Три данных фактора делают трудноприменимым данный вид достаточных условий и требуют их модификации. 4.4.2. Модифицированные достаточные условия ЛУКУ Теорема 4.2. Для того чтобы набор где где – реализация угроз и контругроз, Если показатели имеют смысл показателей эффективности, то знаки второго и третьего неравенств в (4.25) меняются на противоположные. Доказательство приведено в работе [54]. Показано, что если задана постоянная где а из второго и третьего условия (4.25) следует, что управление 4.4.3. Метод оптимизации Условия теоремы 4.2 предполагают, что неравенства (4.25) выполняются на множестве допустимых управлений Если в первом слагаемом множество Один из вариантов методического упрощения структуры алгоритма на втором этапе заключается в сведении исходной задачи к такому виду, когда для получения Для этого вводятся дополнительные координаты и исходная задача сводится к задаче с терминальным показателем где Тогда где последняя система имеет вид В данной трактовке достаточные условия принимают вид системы при наличии связей (4.36) – (4.38). Здесь и далее рассматриваются кусочно-непрерывные скалярные (или векторные а также параметризованные стратегии Таким образом, необходимо найти пару Общую алгоритмическую структуру этапа 2 теперь можно базировать на основе следующей геометрической трактовки. Примем для рассуждений без ограничения общности результата, что размерность систем (4.36) и (4.37) Тогда система (4.39) является системой скалярных неравенств следующего вида (прочерки над переменными опускаем): Вектора a, b являются векторами, однозначно зависящими от u0. Вектора
Рис. 4.2. Топология алгоритма на основе ОД Утверждение 4.4. Для того чтобы третье неравенство системы (4.41) выполнялось на всей Доказательство. Достаточно учесть знак скалярного произведения Утверждение 4.5. Для того чтобы второе неравенство системы (4.41) выполнялось на всей Доказательство базируется на учете знака скалярного произведения Утверждение 4.6.Первое неравенство системы (4.41) ограничивает область допустимых значений нормали aгиперплоскости второго неравенства системы пересечением конусов (–ℓI 0 – ℓII) и (–ℓIV0 – ℓIII), где ℓIII и ℓIV – нормали к гиперплоскостям, касающимся Доказательство. Рассмотрим от обратного нормаль a в зачерченном секторе (–ℓIII0 – ℓIV). Тогда всегда найдется вектор Полученная система конусов (ℓI0ℓII) по b и (–ℓIV0 – ℓI), (–ℓII 0 ℓIII)по а(выделены ярко на рис. 4.2) при данном расположении ОДj является алгоритмической основой для получения Область 1. «Приближаться» к началу координат, разворачивая касательные гиперплоскости. 2. «Вырождаться» в фигуру с малым конусом при вершине при уменьшении угла между касательными гиперплоскостями или увеличении пространственного угла конуса (ℓI0 ℓII). Утверждение 4.7. При касании Доказательство. Действительно, при «приближении» границы Для реализации алгоритма применяется метод моментов Н.Н. Красовского [129], так как он апеллирует к ОД и позволяет найти нормали ℓкасательных к ОД гиперплоскостей. Теорема 4.3[50]. Оптимальное управление, приводящее траекторию в точку касания ОД и гиперплоскости, а также вектор нормали ℓ в точке касания определяются при решении задачи где Доказательство. На основании необходимых и достаточных условий разрешимости задачи об управлении [129, стр. 381], сформулированной в [129] в форме проблемы моментов, область достижимости имеет вид где
Для каждой точки q, лежащей на границе области G, условие (45) выполняется со знаком равенства. Минимизация (4.46) позволяет получить управление, переводящее систему (4.42) из начального состояния в некоторую точку границы G. Вектор нормали ℓ = ℓ0 к гиперплоскости, проведенной в точку касания, определяется из условия максимума равенства в выражении (4.45). Совместное решение этих задач [129, стр. 385] позволяет получить уравнение гиперплоскости (рис. 4.3) В данной задаче
Рис. 4.3. Касательная гиперплоскость к Gx В достаточных условиях рассматриваются лишь касательные гиперплоскости, проходящие через начало координат (рис. 4.2). Поэтому Следовательно, выражение (4.45) для точек границы G принимает вид Раскрывая, при полной позиции m = n получим что и требовалось доказать. В соответствии с полученными результатами общая структура этапа 2 метода оптимизации управлений на основе объединения модифицированных достаточных условий ЛУКУ (МДУ ЛУКУ) и метода моментов Н.Н. Красовского можно представить итерационным процессом, основой которого являются следующие шесть шагов: Шаг 1: приведение исходной постановки к виду (4.34) – (4.38); Шаг 2: формирование системы неравенств (4.39) (МДУ ЛУКУ); Шаг 3: итерация 1: задание начальных приближений итерация i > 1: формирование текущих приближений Шаг 4: формирование системы (4.42) (A,B,X(T,t)) на основе приближений а также соответствующих конусов Шаг 5: решение задачи Парето–оптимизации Шаг 6: а) задача решена, если управление
Рис. 4.4. Итерационная процедура 2-го этапа Структурная схема алгоритма в обобщенном виде приведена на рис. 4.4. 4.5. Применение двухэтапного метода получения 4.5.1. Постановка задачи Рассмотрим этап задачи противодействия локальной системы воздушного нападения (ЛС СВН) и локальной системы ПВО (ЛС ПВО) [173]. Противодействие ЛС СВН – ЛС ПВО состоит в том, что ЛС СВН стремится преодолеть ЛС ПВО для поражения защищаемого объекта, а ЛС ПВО препятствует прорыву. Задача получения программно-корректируемого закона управления активными средствами при взаимодействии ЛС СВН–ЛС ПВО представляет собой итерационную процедуру, на каждой итерации которой выполняются четыре шага [54]: Шаг 1. формирование конфигурации конфликта; Шаг 2. целераспределение АС СВН и ПВО по активным и пассивным средствам ПВО и СВН соответственно; Шаг 3. имитация конфликта; Шаг 4. прогнозирование динамики конфликта. Далее рассматривается упрощенный вариант последнего шага прогноза динамики конфликта (полное исследование задачи дано в главе 10).
Рис. 4.5. Структура взаимодействия в ММС: В данной задаче естественным является поиск таких режимов функционирования ЛС СВН – ЛС ПВО, которые были бы конфликтно-оптимальными. Каждая система состоит из двух подсистем: активной и пассивной. Активные средства каждой коалиции воздействуют на активные и пассивные средства противоположной коалиции. Для ЛС СВН активными средствами являются истребители-перехватчики с ракетами «воздух-земля» и противорадиолокационными ракетами, а для ЛС ПВО – зенитно-ракетные комплексы. Пассивные средства для ЛС СВН – бомбардировщики, для ЛС ПВО – радиолокационные станции [173]. На рис. 4.5 приведена структура взаимодействия сторон. Система задается следующим образом: где Pij – эффективность воздействия одного объекта i-го вида одной системы на один объект j-го типа другой системы, Рассмотрим данную систему в пошаговом варианте. Шаг – конечный интервал времени; число шагов конечно ( Шаг равен В пошаговом варианте система (4.16) преобразуется в систему: Здесь k = 1, 2,..., 0 £ qi £ 1 (i = 1,2), 0 £ Pij £ 1 (i = 1,3; j = 1,2,3,4); xi > 0, xi(k) – численность к началу k-го шага. В качестве показателя терминальных потерь (J) выберем показатель, имеющий смысл суммарного перевеса по активным и пассивным средствам и скорости убывания активных средств «партнера». JА Þ min; JБ Þ min. JА – показатель потерь коалиции А. Чем меньше JА, тем больше выигрыш коалиции А; JБ – показатель потерь коалиции Б. Чем меньше JБ, тем больше выигрыш коалиции Б; aij – весовые коэффициенты, определяющие целевой приоритет каждой стороны в поражении активных или пассивных средств противоположной стороны (терминальная составляющая) или в увеличении интегральной скорости убывания активных средств противника (интегральная составляющая). (0 £aij £ 1; ai1 + a i2 + ai3 = 1; i = {1,2}), значения коэффициентов задаются в зависимости от тактики каждой из сторон. 4.5.2. Применение сетевого подхода для получения Получение начального приближения УКУ. Для реализации сетевого подхода, используя алгоритм общего вида, базирующийся на определении угроз и контругроз, сформирован алгоритм получения сетевых приближений УКУ-решений для двухкоалиционной, двухкритериальной задачи На шаге 1 алгоритма формируется двухмерная ортогональная равномерная сеть (см. рис. 4.1). На шагах 2–8 формируется множество УКУ-оптимальных сетевых решений, которые можно использовать в качестве начальных приближений для 2-го этапа получения оптимального управления ММС. Структура алгоритма (шаги 2–8) показана на рис. 4.6. Реализация сетевого алгоритма УКУ-оптимизации осуществлена в среде ПС МОМДИС [48, 55], а также см. гл. 9. В качестве базового рассматривался следующий вариант: · начальные условия задачи: · эффективности воздействия объектов i-го типа одной системы на объекты j-го типа другой системы: · весовые коэффициенты, определяющие приоритет каждой из систем в поражении активных и пассивных средств противника: · квадратичный критерий (без учета скорости): анализ проводился на двух тактах.
Рис. 4.6. Сетевой алгоритм поиска начальных приближений УКУ-решений На рис. 4.7 показаны область параметров и область показателей для базового варианта. Результаты временных замеров приведены в табл. 4.1.
Рис. 4.7а. Результаты Нэш–Парето–УКУ-оптимизации (область параметров)
Рис. 4.7б. Результаты Нэш–Парето–УКУ-оптимизации (область показателей) Таблица 4.1 Зависимость времени вычисления области УКУ
k = 1,2; Показатели – терминальные квадратичные. Анализ влияния изменения параметров моделей. Исследования проводились в следующих направлениях (глава 10): · влияние соотношения весовых коэффициентов вектора показателей · влияние соотношения численностей объектов · влияние соотношения эффективности воздействия · влияние вида показателей · влияние числа шагов DТ. О пересечении множества УКУ и ПНОК при различных ресурсных соотношениях коалиций. Из анализа прикладных результатов выявляются некоторые общие закономерности, которые сложно получить «прямыми» теоретическими исследованиями. Среди других следует отметить явно проявившуюся тенденцию не единственности УКУ-решений коалиционной дифференциальной игры. При этом большая часть решений находится внутри области Парето–Нэш- компромиссов (ПНОК) (см. гл. 6). Если ресурсы коалиций не равные, то на ПНОК имеем небольшое число точек УКУ, которые смещены в пользу коалиции с большими ресурсами. При выравнивании ресурсов число УКУ-решений увеличивается, а само множество заполняет ПНОК, принимая во многих случаях очертания ПНОК. Следовательно, может быть сформулировано следующее утверждение общего характера, которое обосновывает более общее утверждение 6.10 (гл. 6): Утверждение 4.8 [50]. Парето–Нэш-область компромиссов содержит УКУ-оптимальные решения, а при выравнивании ресурсов коалиций число решений возрастает и их множество существенно пересекается с ПНОК. Причем на большом числе вариантов большая часть Парето-границы ПНОК содержит УКУ-решения. С точки зрения принципа необязательных соглашений Мулена точки Парето-границы могут играть роль начальных приближений при точном отыскании УКУ-решений (см. точку УКУ-СТЭК на рис. 4.7). 4.5.3. Получение точного УКУ-решения на основе МДУ ЛУКУ Получение МДУ ЛУКУ. В соответствии с шагами 1-го и 2-го этапов оптимизации приводим исходную постановку задачи к виду (4.34) – (4.39). Показатели коалиций JA и JБ примут вид (4.34): Тогда из (4.35) – (4.38), учитывая (4.39), получаем где Тогда в соответствии с (4.39) МДУ ЛУКУ принимают следующий вид: · первое неравенство: · второе неравенство: · третье неравенство: Рассмотрим случай, когда Вычисление матрицы перехода. В соответствии с шагом 4 сформируем систему (4.42) для варианта с терминальными показателями, т.е. когда Для упрощения дальнейших вычислений делаем замену Переходная матрица X(T,t) имеет вид где E – единичная матрица. Преобразовав элементы матрицы и используя свойства рядов, получим окончательное выражение для матрицы перехода: Реализация метода моментов Н.Н. Красовского.На шаге 4 УКУ-оптимизации для определения границ конусов нормалей, удовлетворяющих МДУ ЛУКУ, необходимо решить задачу (4.43). Для этого вычислим где ℓ– вектор нормали к ОД, Тогда для При Если F < 0, то максимум выражения (4.58) достигается при Если F ³ 0, то максимум выражения (4.58) достигается при
Окончательно имеем, что нормаль где Таким образом, второе и третье неравенства системы достаточных условий ЛУКУ (4.54) принимают вид: Подобным образом на основе метода моментов можно получить, что вектор нормали для области где Первое неравенство системы достаточных условий ЛУКУ (4.54) принимает следующий вид: Получение УКУ-решений на основе W-оптимизации. Для получения точных УКУ-решений воспользуемся процедурой W-оптимизации программного комплекса МОМДИС. Для реализации этапа 2 оптимизации на основе УКУ в процедуру вычисления необходимо внести изменения. В качестве начального приближения для выполнения процедуры W–оптимизации будем использовать управление В качестве дополнительных ограничений на решения, получаемые в результате W-оптимизации, используются модифицированные достаточные условия ЛУКУ (4.60), (4.62). Данные ограничения реализованы следующим образом. Во время выполнения процедуры W-оптимизации на каждом шаге вычислений все управления, проверяемые процедурой на удовлетворение условий оптимальности, заложенных в методе W-оптимизации, также проверяются и на соблюдение МДУ ЛУКУ. В случае, если данное управление не удовлетворяет МДУ ЛУКУ, то показателю присваивается заведомо не оптимальное значение, и алгоритм «отбраковывает» данное решение, повторяя итерацию для поиска другого варианта. Результаты W-оптимизации с проверкой на ЛУКУ-оптимальность представлены на рис. 4.8.

 
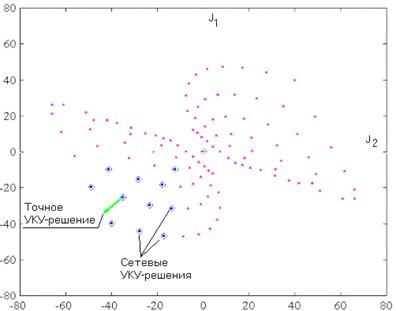
Рис. 4.8. Точное решение УКУ-оптимизации Получение УКУ-решений дифференциальной игры.Для того, чтобы набор Таким образом, для того, чтобы набор Отсюда аналогично случаю для одной коалиции получаем на основе метода момента Н.Н. Красовского систему из шести неравенств, выполнение которых будем проверять для получения точных УКУ-решений дифференциальной игры. Проверяя неравенства во время выполнения процедуры W-оптимизации, получаем решение дифференциальной игры, которое в данной задаче совпадает с решением для коалиции K (рис. 4.8). Это является следствием того факта, что сетевые решения – начальные приближения УКУ-решений дифференциальной игры. Таким образом реализуется двухэтапный метод определения УКУ-решения. На первом этапе приближенного сетевого анализа на множестве показателей практически решается вопрос существования УКУ-решений, в частности, для рассмотренной конфликтной задачи было обнаружено, что множество УКУ-решений имеет существенное пересечение с Парето–Нэш- областью компромиссов. На втором этапе вновь решается задача определения точных Данный метод формирует класс стабильно-эффективных компромиссов (СТЭК) на базовом Парето–Нэш-множестве компромиссов. СТЭК на основе УКУ обладает дополнительной эффективностью по сравнению с Нэш-решением и сохраняет свойства равновесной стабильности в условиях необязательных соглашений. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 725. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 коалиций вида
коалиций вида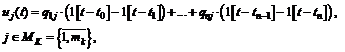 (4.16а)
(4.16а)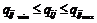 , а
, а  и
и  определяются значениями сети параметров
определяются значениями сети параметров  .
. . (4.16б)
. (4.16б) (4.17)
(4.17)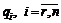 определяется множество (n – r) равномерных ортогональных сетей точек размерности mK и густоты
определяется множество (n – r) равномерных ортогональных сетей точек размерности mK и густоты 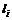 , на множестве которых и вычисляются области стабильного по УКУ взаимодействия коалиций [55].
, на множестве которых и вычисляются области стабильного по УКУ взаимодействия коалиций [55]. отображаются в пространство показателейJ, формируя таким образом ее допустимый вид.
отображаются в пространство показателейJ, формируя таким образом ее допустимый вид.
 , сеть формируется перед началом игры и остается неизменной при взаимодействии (не зависит от i).
, сеть формируется перед началом игры и остается неизменной при взаимодействии (не зависит от i). и точек сети
и точек сети  определяется из выражения
определяется из выражения ,
, – размерность области параметров q; li – густота сети на i-м шаге;
– размерность области параметров q; li – густота сети на i-м шаге;  – нижняя и верхняя границы i-й компоненты
– нижняя и верхняя границы i-й компоненты  вектора параметров.
вектора параметров. .
.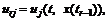 где
где  . Очевидно обобщение сетей для векторных управлений коалиций
. Очевидно обобщение сетей для векторных управлений коалиций 
 и
и 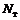 для
для  ;
; проверяется наличие «угрозы» коалиции K, т.е. точки с координатами
проверяется наличие «угрозы» коалиции K, т.е. точки с координатами  , для которой выполняется условие (4.9);
, для которой выполняется условие (4.9);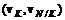 , для которой выполняются условие (4.10); б) если «угрозы» не существует, то переходим на шаг 6б;
, для которой выполняются условие (4.10); б) если «угрозы» не существует, то переходим на шаг 6б;
 ,
, , (4.18)
, (4.18) . (4.19)
. (4.19) . (4.20)
. (4.20) обладает свойствами [32]:
обладает свойствами [32]: существует единственное решение
существует единственное решение  системы (4.20);
системы (4.20);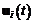 являются кусочно-непрерывными функциями, имеющими конечное число точек разрыва (свойства 1, 2 определяют множество
являются кусочно-непрерывными функциями, имеющими конечное число точек разрыва (свойства 1, 2 определяют множество  )
) ;
; ;
; при
при  управление
управление  также принадлежит
также принадлежит  ,
, – малая положительная константа.
– малая положительная константа. (или
(или  по некоторым
по некоторым  из
из  или из
или из  ) является возможность замены коалицией K управления uK(t) на
) является возможность замены коалицией K управления uK(t) на  ,
,  так, чтобы
так, чтобы . (4.21)
. (4.21) на
на  ,
,  так, чтобы
так, чтобы ,
, . (4.22)
. (4.22) , для которого существует постоянная e > 0 такая, что на любую локальную угрозу коалиции K у контркоалиции N/K имеется локальная контругроза.
, для которого существует постоянная e > 0 такая, что на любую локальную угрозу коалиции K у контркоалиции N/K имеется локальная контругроза.
 , а gK,gN/K – постоянные.
, а gK,gN/K – постоянные. имеет место:
имеет место: . (4.23)
. (4.23) (4.24)
(4.24) (j = K, N/K) – матрицы Якоби, Y(t) – матрица фундаментальных решений. Далее для удобства будем обозначать УКУ-решение, как
(j = K, N/K) – матрицы Якоби, Y(t) – матрица фундаментальных решений. Далее для удобства будем обозначать УКУ-решение, как  .
. было локальной угрозой и контругрозой для коалиции K, достаточно, чтобы
было локальной угрозой и контругрозой для коалиции K, достаточно, чтобы имело место неравенство
имело место неравенство  , где
, где  – скалярное произведение,
– скалярное произведение,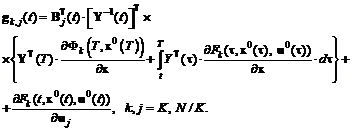
 ,
, ,
, 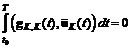
 , которое не должно входить в
, которое не должно входить в  , для всех
, для всех  решения нет, при этом ядро уравнения gK,K(t) имеет сложный вид.
решения нет, при этом ядро уравнения gK,K(t) имеет сложный вид. системы (4.24).
системы (4.24). был локальной угрозой и контругрозой для коалиции K, достаточно, чтобы для любых допустимых
был локальной угрозой и контругрозой для коалиции K, достаточно, чтобы для любых допустимых  выполнялась система неравенств:
выполнялась система неравенств: , (4.25)
, (4.25) (4.26)
(4.26)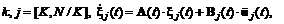 (4.27)
(4.27) (4.28)
(4.28)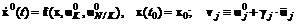 (4.29)
(4.29) принадлежат
принадлежат  , вектор малых величин gj выбираем из условия
, вектор малых величин gj выбираем из условия , где
, где 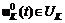 и
и  условия теоремы выполняются, то, введя допустимые вариации управлений,
условия теоремы выполняются, то, введя допустимые вариации управлений,
 и
и 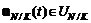 , из первого условия (4.25) следует, что управление
, из первого условия (4.25) следует, что управление  реализует локальную угрозу коалиции K
реализует локальную угрозу коалиции K , (4.31)
, (4.31) реализует контругрозу
реализует контругрозу . (4.32)
. (4.32) коалиции
коалиции  . Следовательно, каждое из трех скалярных произведений выражения (4.26) представляет собой произведение вектора, зависящего от оптимального управления и траектории, на любой вектор из допустимого множества.
. Следовательно, каждое из трех скалярных произведений выражения (4.26) представляет собой произведение вектора, зависящего от оптимального управления и траектории, на любой вектор из допустимого множества. имеет смысл множества достижимости при t = T [129], то в интегральном члене (4.26) имеет место ансамбль траекторий
имеет смысл множества достижимости при t = T [129], то в интегральном члене (4.26) имеет место ансамбль траекторий  и множество управлений
и множество управлений 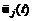 .
. достаточно использовать лишь области достижимости.
достаточно использовать лишь области достижимости. (4.33)
(4.33) , (4.34)
, (4.34) – расширенный вектор.
– расширенный вектор. (4.35)
(4.35) ; (4.36)
; (4.36) , (4.37)
, (4.37) (4.38)
(4.38) (4.39)
(4.39) ) управления
) управления  , (4.40)
, (4.40) .
. , которая на множествах допустимых управлений
, которая на множествах допустимых управлений  и
и  и, как следствие, на множествах
и, как следствие, на множествах  обеспечивает систему неравенств (4.39).
обеспечивает систему неравенств (4.39).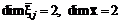 .
. (4.41)
(4.41) заполняют соответствующие области достижимости (ОД) (рис. 4.2).
заполняют соответствующие области достижимости (ОД) (рис. 4.2).
 , достаточно, чтобы вектор нормали bгипер-
, достаточно, чтобы вектор нормали bгипер-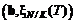 при всех возможных положениях векторов
при всех возможных положениях векторов  в
в  .
. при всех
при всех  .
.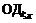 и конуса (–ℓII 0 ℓIII).
и конуса (–ℓII 0 ℓIII). , который обеспечит равенство
, который обеспечит равенство  , т.е.
, т.е.  .
. из достаточных условий теоремы 4.2.
из достаточных условий теоремы 4.2. к началу координат касательные гиперплоскости «расходятся», конический угол (ℓI0 ℓII) уменьшается и в «момент» касания направление ℓI и ℓII совпадает и внутренних точек не имеется, а следовательно, решения нет. Если начало координат попадает внутрь области ОД, то не существует касательных гиперплоскостей, проходящих через начало координат, и решение отсутствует.
к началу координат касательные гиперплоскости «расходятся», конический угол (ℓI0 ℓII) уменьшается и в «момент» касания направление ℓI и ℓII совпадает и внутренних точек не имеется, а следовательно, решения нет. Если начало координат попадает внутрь области ОД, то не существует касательных гиперплоскостей, проходящих через начало координат, и решение отсутствует. системы
системы (4.42)
(4.42) , (4.43)
, (4.43)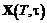 – матрица фундаментальных решений системы (матрица перехода):
– матрица фундаментальных решений системы (матрица перехода): . (4.44)
. (4.44)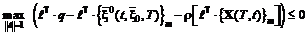 , (4.45)
, (4.45)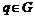 – ограниченное, выпуклое, замкнутое множество ОД,
– ограниченное, выпуклое, замкнутое множество ОД, ,
, – начальные условия,
– начальные условия,  – возмущение, приложенное к системе (4.42), ℓ – некоторый вектор
– возмущение, приложенное к системе (4.42), ℓ – некоторый вектор  , m – размерность G в позиционной задаче управления (m – размерность позиции),
, m – размерность G в позиционной задаче управления (m – размерность позиции),
 . (4.46)
. (4.46) .
. , возмущение
, возмущение  не учитывается, поэтому
не учитывается, поэтому  .
.
 и
и  .
. .
. ,
, и «ячейки»
и «ячейки»  допустимых значений
допустимых значений  на основе сетевых решений этапа 1;
на основе сетевых решений этапа 1;
 ; решение задачи (4.43) для определения границ конусов нормалей Con ℓ (рис. 4.2), удовлетворяющих МДУ ЛУКУ:
; решение задачи (4.43) для определения границ конусов нормалей Con ℓ (рис. 4.2), удовлетворяющих МДУ ЛУКУ:
 , образованных векторами
, образованных векторами  касательных к ОДx;
касательных к ОДx; ; –
; –  , т.е. удовлетворяют системе неравенств (4.39) МДУ ЛУКУ при
, т.е. удовлетворяют системе неравенств (4.39) МДУ ЛУКУ при 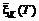 и
и  – векторах касательных, соответствующих ОДx и являющихся границами множеств
– векторах касательных, соответствующих ОДx и являющихся границами множеств  ;
; внутри «ячейки»
внутри «ячейки» 

 (4.47)
(4.47) ; qi – доли активных средств воздействия на активные средства партнера,
; qi – доли активных средств воздействия на активные средства партнера,  ; (1 – qi) – доля активных средств воздействия на пассивные средства партнера;
; (1 – qi) – доля активных средств воздействия на пассивные средства партнера; 
 ). Каждое активное средство делает на шаге один ход.
). Каждое активное средство делает на шаге один ход. .
. (4.48)
(4.48)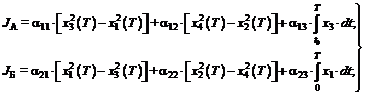 (4.49)
(4.49) ;
; ;
; ;
; ,
,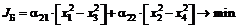 ;
;




 .
. (приближенное положение Парето-оптимальной точки УКУ-СТЭК на ПНОК, данное на рис. 4.7, полностью отражает тактические свойства конфликта (
(приближенное положение Парето-оптимальной точки УКУ-СТЭК на ПНОК, данное на рис. 4.7, полностью отражает тактические свойства конфликта (  ), когда ЛС СВН стремится к поражению АС ЛС ПВО (прорыву ЛС ПВО), а ЛС ПВО стремится в основном к поражению ПС ЛС СВН (защите объектов));
), когда ЛС СВН стремится к поражению АС ЛС ПВО (прорыву ЛС ПВО), а ЛС ПВО стремится в основном к поражению ПС ЛС СВН (защите объектов));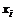 ;
; ;
; ;
; (4.50)
(4.50) , (4.51)
, (4.51) ,
, ; (4.52)
; (4.52) (4.53)
(4.53)


 (4.54)
(4.54)
 , т.е. интегральная часть показателей JA и JБ не учитывается.
, т.е. интегральная часть показателей JA и JБ не учитывается. , (4.55)
, (4.55) . (4.56)
. (4.56) .
. ,
,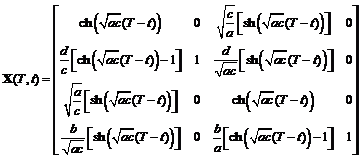 . (4.57)
. (4.57)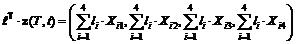 ,
, , используя второе выражение (4.43), имеем
, используя второе выражение (4.43), имеем .
. ,0 < q2 < 1 получим
,0 < q2 < 1 получим (4.58)
(4.58) , а при xБ(t0) = 0 имеем xБ(T) = 0, при котором второе и третье неравенство системы (4.54) не выполняются.
, а при xБ(t0) = 0 имеем xБ(T) = 0, при котором второе и третье неравенство системы (4.54) не выполняются. и на втором этапе решения имеем задачу
и на втором этапе решения имеем задачу  . Решением этой задачи является
. Решением этой задачи является  . Раскроем последнее выражение:
. Раскроем последнее выражение:
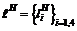 удовлетворяет выражению
удовлетворяет выражению , (4.59)
, (4.59) ,
, ,
, ,
, ,
, – вектор касательной к
– вектор касательной к  (4.60)
(4.60) удовлетворяет выражению
удовлетворяет выражению , (4.61)
, (4.61) ,
, ,
, ,
, .
. . (4.62)
. (4.62) , полученное на этапе 1 вычисления УКУ-решений. В качестве ограничений на управление зададим такую
, полученное на этапе 1 вычисления УКУ-решений. В качестве ограничений на управление зададим такую 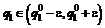 ,
,  , чтобы допустимые управления находились внутри «клеточки», образованной ближайшими узлами ортогональной равномерной сети, используемой на этапе 1.
, чтобы допустимые управления находились внутри «клеточки», образованной ближайшими узлами ортогональной равномерной сети, используемой на этапе 1.