
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Равнобедренный и равносторонний треугольник, их свойства.
Билет №1.
- Смежные и вертикальные углы, их свойства.
- Теорема Пифагора. Пропорциональные отрезки в прямоугольном треугольнике.
Ответы:
1. Смежными углами называют углы, у которых одна сторона общая, а две другие являются дополнительными лучами.
Теорема о смежных углах: Сумма смежных углов равна 180°.

Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого угла.
Теорема о вертикальных углах: Вертикальные углы равны.

- Теорема Пифагора

| Теорема Пифагора. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
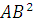 = =  + + 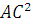 или или  + +  = = 
|
Пропорциональные отрезки в прямоугольном треугольнике
Билет №2
1. Треугольник. Признаки равенства треугольников.
2. Касательная к окружности. Теорема о касательной к окружности.
Ответы:
1.Треугольникомназывается фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки.

| Пишут: Δ АВС. Читают: «треугольник АВС». Углы треугольника при его вершинах обозначают <А (или <ВАС), <В (или <АВС), <С (или <АСВ) и называют внутренними углами треугольника. Стороны треугольника, лежащие против вершин А, В и С, соответственно обозначаются буквами а, bи с, т.е. ВС = а, АС = b, АВ = с.
| | Равными треугольниками называются треугольники, у которых все соответственные стороны равны и все соответственные углы равны.
| 
| 1-й признак равенства треугольников.
Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
| 
| 2-й признак равенства треугольников.
Если одна сторона и прилежащие к ней два угла одного треугольника равны соответствующей стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
| 
| 3-й признак равенства треугольников.
Если три стороны одного треугольника равны трём соответственным сторонам другого треугольника, то такие треугольники равны.
|
Касательная к окружности. Теорема о касательной к окружности

| Касательной к окружности называют прямую, которая имеет одну общую точку с окружностью. Общая точка касательной и окружности называется точкой касания.
Теорема:Касательная к окружности перпендикулярна её радиусу, проведённому в точку касания.
|
Билет №3
1. Равнобедренный и равносторонний треугольник, их свойства.
2. Свойства отрезков касательных, проведенных к окружности из одной точки.
Ответы:
Равнобедренный и равносторонний треугольник, их свойства.

| 
| Равнобедренным треугольником называют треугольник, у которого длины двух сторон равны. Эти равные стороны называют боковыми сторонами, а третью сторону называют основанием равнобедренного треугольника.
| 
| Равносторонним называют треугольник, имеющий равные стороны.
| | Свойства равнобедренного и равностороннего треугольников
| | 
| 1) Теорема. Углы при основании равнобедренного треугольника равны.
2) Теорема (обратная). Если два угла треугольника равны, то он является равнобедренным треугольником
3)В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
4)В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой.
5)В равнобедренном треугольнике биссектриса, проведенная к основанию, является высотой и медианой.
| | 2.Свойства отрезков касательных, проведенных к окружности из одной точки.
| | 
| Если из точки М, лежащей вне окружности с центром в точке О, провести две касательные МВ и МС, то:
1)центр окружности лежит на биссектрисе МО угла ВМС (О ∈ ОМ);
2)расстояния от вершины угла ВМС до точек касания равны (МВ = МС);
3)Отрезки, соединяющие точки касания с центром окружности, являются её радиусами и перпендикулярны к сторонам угла ВМС (ОВ = ОС = R, OB ⟘ MВ, OC ⟘ MС)
4) <ВМС +< ВОС = 180°.
| | | | | |
Билет №4
1. Внешний угол треугольника. Свойство внешнего угла треугольника. Сумма углов треугольника
2. Параллелограмм. Свойства параллелограмма. Площадь параллелограмма.
Билет №5
1. Соотношения между сторонами и углами треугольника. Неравенство треугольника.
2. Прямоугольник. Свойства прямоугольника. Площадь прямоугольника.
3. Внешний угол треугольника. Свойство внешнего угла треугольника. Сумма углов треугольника

| Внешним углом треугольника называют угол, смежный с его внутренним углом. Внешний угол треугольника ( <4) равен сумме двух внутренних, не смежных с ним, т. е. <4= <1+< 2.
Внешний угол треугольника больше любого из внутренних углов, не смежных с ним.
Сумма внутренних углов любого треугольника составляет 180°, т. е. <1+ <2+ <3=180°.
| | 2.Параллелограмм. Свойства параллелограмма. Площадь параллелограмма.
| 
| Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны (AB || CD; AD || BC).
| 
| Свойства параллелограмма
1)У параллелограмма противоположные стороны равны: AB=CD и BC=AD
2)У параллелограмма противолежащие углы равны.
<A=<C и <B=<D
3) Сумма углов параллелограмма, прилежащих к одной его стороне, равна 180°.
Например: <A+<B =180°. <C +<B=180°.
4)Диагонали параллелограмма в точке пересечения делятся пополам
| 
|
Билет №5
1. Соотношения между сторонами и углами треугольника. Неравенство треугольника.
2. Прямоугольник. Свойства прямоугольника. Площадь прямоугольника.
Ответы:
| 1. Соотношения между сторонами и углами треугольника. Неравенство треугольника.
| | 
| Треугольникомназывается фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки.
Пишут: Δ АВС. Читают: «треугольник АВС». Углы треугольника при его вершинах обозначают <А (или <ВАС), <В (или <АВС), <С (или <АСВ) и называют внутренними углами треугольника. Стороны треугольника, лежащие против вершин А, В и С, соответственно обозначаются буквами а, bи с, т.е. ВС = а, АС = b, АВ = с.
1.Периметром треугольника называется сумма всех его сторон. P = a+b+c, где P– периметр, а, bи с– стороны треугольника.
2.В любом треугольнике против большей стороны лежит больший угол.
3.В любом треугольнике против большего угла лежит большая сторона.
4. Любая сторона треугольника меньше суммы двух других его сторон.
| | 2. Прямоугольник. Свойства прямоугольника. Площадь прямоугольника.
| 

| Прямоугольник – это параллелограмм, в котором все углы прямые.
Прямоугольник обладает всеми свойствами параллелограмма. А именно:
1) В прямоугольнике противоположные стороны равны
2) Диагонали в точке пересечения делятся пополам
Свойство прямоугольника
Диагонали прямоугольника равны
| 

|
Площадь прямоугольника равна произведению его смежных сторон.
S = a ∙b.
Площадь прямоугольника равна половине квадрата его диагонали, умноженной на синус угла между диагоналями:
S =   sinα sinα
|
| | | | |
Билет №6
- Параллельные прямые. Признаки параллельности прямых.
- Подобные треугольники. Теорема об отношении площадей подобных треугольников.
| 1. Параллельные прямые. Признаки параллельности прямых.
| 
| Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Запись a || b читается «прямая апараллельна прямой b».
Аксиома параллельности. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
| 
| При пересечении прямых аи bпрямой с(с– секущая) образуется 8 углов, которые рассматривают парами:
внутренние накрест лежащие: <6 и <4; <3 и <5;
внешние накрест лежащие: <1 и <7; <2 и <8;
соответственные: <1 и <5; <4 и <8;
<2 и <6; <3 и <7
внутренние односторонние: <4 и <5; <3 и <6
внешние односторонние: <1 и <8; <2 и <7
Признаки параллельности прямых:
1) Если внутренние накрест лежащие углы, образованные двумя прямыми и секущей, равны, то эти две прямые параллельны.
2) Если при пересечении двух прямых третьей соответственные углы равны, то данные две прямые параллельны.
3) Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то данные две прямые параллельны.
| | 2.Подобные треугольники. Теорема об отношении площадей подобных треугольников.
| 
| Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Для обозначения подобия фигур используется специальный значок: ∾. Так как преобразование фигуры F в фигуру F1 является преобразованием подобия, то можно записать: F ∾ F1.Читают: фигура F подобна фигуре F1.
У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны.
У подобных треугольников соответствующие углы равны и стороны одного треугольника пропорциональны соответственным сторонам другого треугольника.
Пишут: ∆ АВС ∾ ∆ А1В1С1.
Читают: треугольник АВС подобен треугольнику А1В1С1. Это значит, что < А =< А1, <В =< В1, <С = <С1 и
 =k, где k– коэффициент подобия и равен отношению соответственных сторон этих треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. =k, где k– коэффициент подобия и равен отношению соответственных сторон этих треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. 
|
Билет №7
1. Свойства углов, образованных при пересечении параллельных прямых секущей.
2. Ромб. Свойства ромба. Площадь ромба.
Ответы:
| 1. Свойства углов, образованных при пересечении параллельных прямых секущей
| | 
| При пересечении прямых аи bпрямой с(с– секущая) образуется 8 углов, которые рассматривают парами:
внутренние накрест лежащие: <6 и <4; <3 и <5;
внешние накрест лежащие: <1 и <7; <2 и <8;
соответственные: <1 и <5; <4 и <8;
<2 и <6; <3 и <7
внутренние односторонние: <4 и <5; <3 и <6
внешние односторонние: <1 и <8; <2 и <7
Свойства параллельных прямых.
1) Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны.
2)Если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180°.
3)Если две параллельные прямые пересечены секущей, то соответственные углы равны.
| | 2. Ромб. Свойства ромба. Площадь ромба.
| 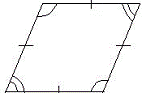

| Ромб – это параллелограмм, у которого все стороны равны.
Ромб обладает всеми свойствами параллелограмма. А именно:
1) В ромбе противоположные стороны равны
2) Диагонали в точке пересечения делятся пополам
Свойство ромба
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
| 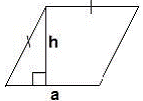
| Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне:
S = a ∙h.
| 
|
Площадь ромба равна произведению квадрата его стороны на синус угла: S= 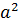 sinβ. sinβ.
| 
| Площадь ромба равна половине произведения его диагоналей: S=  
| | | | |
Билет №8
1. Прямоугольный треугольник, его свойства. Площадь прямоугольного треугольника.
2. Признаки подобия треугольников.
Ответы:
| 1. Прямоугольный треугольник, его свойства. Площадь прямоугольного треугольника.
| 
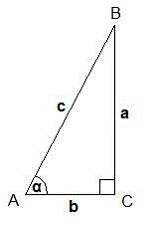
| Прямоугольным называют треугольник, у которого один угол прямой (равен 90°). Стороны прямоугольного треугольника имеют особые названия: катеты (стороны, образующие прямой угол), и гипотенуза (сторона, лежащая против прямого угла).
1) Каждый катет прямоугольного треугольника меньше его гипотенузы.
2) У треугольника не может быть больше одного прямого угла.
3) Сумма острых углов прямоугольного треугольника равна 90°.
| 
|
Площадь прямоугольного треугольника равна половине произведения его катетов: SΔ =  a ∙b. a ∙b.
|
| | 2. Признаки подобия треугольников
| 
| 1)Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2)Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
3)Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
|
Билет №9
- Признаки равенства прямоугольных треугольников.
- Средняя линия трапеции. Площадь трапеции.
Ответы:
| 1. Признаки равенства прямоугольных треугольников.
| | 
|
1)Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
| | 
| 2)Если один катет и прилежащий к нему угол одного прямоугольного треугольника соответственно равны одному катету и прилежащему к нему углу другого прямоугольного треугольника, то такие треугольники равны.
| | 
|
3)Если гипотенуза и один острый угол одного прямоугольного треугольника соответственно равны гипотенузе и одному острому углу другого прямоугольного треугольника, то такие треугольники равны.
| | 
| 4)Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
| | 2. Средняя линия трапеции. Площадь трапеции
| 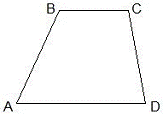
| Трапецией называют четырёхугольник, две стороны которого параллельны между собой, а две нет. Две параллельные стороны называют основаниями трапеции, а две другие стороны называют боковыми сторонами трапеции.
ABCD – трапеция, AD и ВС – основания (AD ||ВС), АВ и CD – боковые стороны трапеции.
| 
| Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции. В трапеции AВСD отрезок MN - средняя линия.
Теорема о средней линии трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме. В трапеции AВСD средняя линия MN || AD, MN || BC;
MN = . 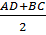
| 
| Площадь трапецииравна произведению полусуммы её оснований на высоту трапеции или площадь трапеции равна произведению её средней линии на высоту:
S = .  или S = MN ∙BF. или S = MN ∙BF.
| | | | |
Билет №10
- Трапеция. Равнобедренная трапеция, прямоугольная трапеция. Свойства равнобедренной трапеции.
- Центральный угол, вписанный угол. Свойства вписанных углов. Теорема о вписанном угле.
Ответы:
| 1. Трапеция. Равнобедренная трапеция, прямоугольная трапеция. Свойства равнобедренной трапеции.
| 
| Трапецией называют четырёхугольник, две стороны которого параллельны между собой, а две нет. Две параллельные стороны называют основаниями трапеции, а две другие стороны называют боковыми сторонами трапеции.
ABCD – трапеция, AD и ВС – основания (AD ||ВС), АВ и CD – боковые стороны трапеции.
| 
| Трапецию называют равнобокой или равнобедренной, если её боковые стороны равны между собой. Трапеция PKEF является равнобокой, так как её боковые стороны PK и EF равны.
У равнобокой трапеции углы при основании равны
<P=<F и <K=<E
| 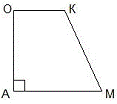
| Прямоугольной называют трапецию, имеющую прямой угол.
Трапеция АОКМ – прямоугольная, так как угол А – прямой. Угол О также будет прямым.
| | 2.Центральный угол, вписанный угол. Свойства вписанных углов. Теорема о вписанном угле.
| 

| Угол, образованный двумя радиусами, называется центральным углом окружности (угол с вершиной в центре окружности) < АОВ – центральный.
Центральный угол измеряется величиной дуги, на которую он опирается. ᴗAnB=90° и центральный <АОВ=90°
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. <АСВ-вписанный
Теорема:Вписанный угол измеряется половиной дуги, на которую он опирается.
Например, ᴗAnB=90°, а вписанный <АСВ=45°.
Следствия:
1)Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой.
2)Вписанный угол, опирающийся на диаметр, равен 90°. Вписанный угол MNP опирается на диаметр МР, который стягивает дугу в 180° (полуокружность), поэтому,< MNP=90°.
|
Билет №11
1. Средняя линия треугольника. Теорема о средней линии треугольника.
2.Окружность, описанная около треугольника. Центр окружности, описанной около треугольника. Центр окружности, описанной около прямоугольного треугольника.
Ответы:
| 1. Средняя линия треугольника. Теорема о средней линии треугольника
| | 
| Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
MN – средняя линия треугольника АВС.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна третьей стороне и равна её половине. MN || AC; MN =  AC AC
| | 2.Окружность, описанная около треугольника. Центр окружности, описанной около треугольника. Центр окружности, описанной около прямоугольного треугольника.
| 


| Окружность называется описанной около треугольника, если она проходит через все его вершины.
Центр окружности, описанной около треугольника, есть точка пересечения серединных перпендикуляров к сторонам треугольника.
Центр окружности, описанной около остроугольного треугольника лежит внутри треугольника (рисунок слева).
Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы (рисунок в центре).
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (рисунок справа).
| | | | |
Билет №12
1. Медиана треугольника. Теорема о медианах треугольника.
2. Свойство сторон четырехугольника, описанного около окружности
Ответы:
| 1.Медиана треугольника. Теорема о медианах треугольника.
| | 
| Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Все три медианы любого треугольника пересекаются в одной точке, лежащей внутри треугольника, которая делит их в отношении 2 : 1, считая от вершины треугольника.
OE =  OB; OD = OB; OD =  OA; OF = OA; OF =  OC
В треугольнике АВС медианы AD, BE и CF пересекаются в точке О. OC
В треугольнике АВС медианы AD, BE и CF пересекаются в точке О.
| | 2. Свойство сторон четырехугольника, описанного около окружности
| 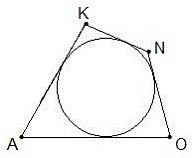
| Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Четырёхугольник AKNO является описанным около окружности.
1)В описанном четырёхугольнике суммы противоположных сторон равны. (AO+KN=AK+ON).
2)Если в выпуклом четырёхугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
| | | | |
Билет №13
1. Синус, косинус, тангенс острого угла прямоугольного треугольника. Значение синуса ,косинуса и тангенса для углов 
2. Признаки параллелограмма.
Ответы:
Билет №14
1.Биссектриса угла. Свойство биссектрисы угла.
2. Теорема синусов. Теорема косинусов
Ответы:
Билет №15
1.Формулы площади треугольника
2.Окружность, вписанная в треугольник. Центр окружности, вписанной в треугольник.
Ответы:
| 1. Формулы площади треугольника
| 
|
| Площадь прямоугольного треугольника равна половине произведения его катетов:
| SΔ =  ab ab
| 
| Площадь любого треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: SΔ ==  ah ah
| 
| Площадь любого треугольника равна половине произведения двух его сторон на синус угла между этими сторонами: SΔ =  a ∙b ∙sinγ a ∙b ∙sinγ
| 
| Площадь равностороннего треугольника со стороной анаходят по формуле:
SΔ = 
| 
| Если известны все три стороны треугольника, то его площадь можно найти по формуле Герона:
SΔ =  ,
где p = ,
где p =  - полупериметр - полупериметр
| 
|
Площадь треугольника равна половине произведения его периметра Рна радиус вписанной окружности r(центр окружности, вписанной в треугольник, лежит на пересечении биссектрис углов треугольника).
SΔ =  Pr, где P = a+b+c - периметр Pr, где P = a+b+c - периметр
|
| | 2. Окружность, вписанная в треугольник. Центр окружности, вписанной в треугольник.
| 
| Окружность называется вписанной в треугольник, если она касается всех его сторон.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
|
Билет№16
- Серединный перпендикуляр к отрезку. Свойство серединного перпендикуляра к отрезку.
2. Свойство углов четырехугольника вписанного в окружность.
Ответы:
| 1. Серединный перпендикуляр к отрезку. Свойство серединного перпендикуляра к отрезку
| 
| Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему. ОС – серединный перпендикуляр к отрезку АВ
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. ОС – серединный перпендикуляр к отрезку АВ. АС = ВС.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
| | 2. Свойство углов четырехугольника, вписанного в окружность.
| 
| Многоугольник называется вписанным в окружность, если все его вершины лежат на этой окружности. Четырёхугольник ABCD является вписанным в окружность.
1)Сумма противоположных углов вписанного четырёхугольника равна 180°. ( А+ С= В+ D=180°).
|
|





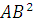 =
=  +
+ 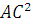 или
или  +
+  =
= 

 =
=  или
или  =AD·BD
=AD·BD
 =
=  или
или  =AB·AD
Аналогично,
=AB·AD
Аналогично,  =
=  или
или  =AB·BD
Примечание. Утверждения 1 и 2 следуют из подобия прямоугольных треугольников АВС, ADC и BDC.
=AB·BD
Примечание. Утверждения 1 и 2 следуют из подобия прямоугольных треугольников АВС, ADC и BDC.



















 sinα
sinα



 =k, где k– коэффициент подобия и равен отношению соответственных сторон этих треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
=k, где k– коэффициент подобия и равен отношению соответственных сторон этих треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. 




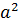 sinβ.
sinβ.



 a ∙b.
a ∙b.






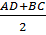

 или S = MN ∙BF.
или S = MN ∙BF. 





 AC
AC




 OB; OD =
OB; OD = 

 или sinα =
или sinα = 


 (
(  )
) или tgα =
или tgα = 
 )
)

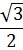






 Теорема: Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Теорема: Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

 В теореме синусов каждое из трёх отношений
В теореме синусов каждое из трёх отношений  ,
,  ,
,  равно 2R, где R – радиус окружности, описанной около треугольника.
равно 2R, где R – радиус окружности, описанной около треугольника.
 = 2R
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними:
= 2R
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними:
 +
+  – 2b cosα
– 2b cosα

 ab
ab




 ,
где p =
,
где p =  - полупериметр
- полупериметр



