
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторы и операции над ними. Векторы в трёхмерном пространстве. Векторный и координатный методы решения задач.Стр 1 из 2Следующая ⇒ Неевклидовы геометрии. Общие вопросы аксиоматики. Особенности плоскости Лобачевского. Метрика. Модели плоскости.
Вся геометрия Лобач-го основана на V постулате Лобач-го: Пусть а-призволь-я прямая, а А-точка,не лежащая на этой прямой.Тогда в пл-ти,орпедел-й точкой А и пр-й а,сущ-т не менее 2-х пр-х,прох-х через т.А и не пересек-х пр-ю а. На пл-ти Лоб-го имеют место след-е случаи взаим-го распол-я прям-х:1)параллель-е2)расход-ся3)пересек-ся. Т1.если пр-е АВ и СД не имеют общ-х точек и сущ-т точки Р и Q такие ,что РÎАВ и QÎСД,и люб-й внутр-й луч угла QРВÇ луч QД, то АВ¤¤СД. Т2.Пусть АВ-произв-я напрвлен-я пр-я,а М-точка, не леж-я на ней.Тогда в пл-ти МАВ сущ-т одна и только одна пр-я СД, проход-я через Т.М и параллель-я пр-й АВ.Лемма.Если АВ//СД, то сущ-т ось симм-и пр-х АВ и СД. Т3.а)Если АВ//СД, то СД//АВ.б)Если АВ//ЕF,ЕF//СД и пр-е АВ и СД не совпад-т, то АВ//СД. Пр-я АВ наз-ся параллельной прямой СД, если эти рп-е не имеют общих точек и, каковы бы ни были точки Р и Q,леж-е соответ-о на пр-х АВ и СД,любой внутренний луч угла QРВ Çлуч ОД. Если определить конкретное направление прямой а (например прямые АВ и ВА рассматривать как две различные прямые), то и каждую точку М, не лежащую на данной прямой а, проходят две прямые, параллельные прямой а в двух разных направ-х. Эти 2 прямые образ-т рав-е острые углы с перпендикуляром MN, проведенным из точки М к прямой а. Каждый из них называется углом параллельности в точке М относительно прямой а. Т5.Две прямые на плоскости Лобачевского называются расходящимися (или сверхпараллельными), если они не пересекаются и не параллельны. Т.6.Две прямые, имеющие общий перпендикуляр, расходятся.  Расходящиеся прямые неограниченно расходятся друг от друга по мере удаления от общего перпендикуляра, а параллельные прямые неограниченно удаляясь друг от друга в одном направлении асимптотически приближаются в другом. Для доказательства непротиворечивости системы аксиом плоскости Лобачевского необходимо иметь представление о таких моделях плоскости Лобачевского, как модель на псевдосфере(модель в круге).Все доказательства непротиворечивости геометрии Лобачев-го имеют услов-й хар-р:Геом-я Лоб-го не может содержать противоречий, если их не содержит Евклид-а Для построение арифметической модели отождествим геометрическую плоскость с координатной плоскостью, точками которой являются пары чисел (х, у) - координаты точки, а прямые описываются уравнением у=кх+в или х=а. Модель Пуанкаре геометрии Лоб-го.Роль полупл-ти Лоб-го играет открытая полупл-ть, за роль прям-х-примем содерж-ся в ней полуокр-ти,с центрами на огранич-ей ее прямой и лучи,^этой пр-й.Все аксиомы Евклид-й геом-ии выпол-ся кроме аксиомы параллельных,Þв этой модели выпол-ся геом-я Лоб-го. За угол примем фигуру из 2 лучей с общим началом,не содер-ся в одной прямой.(рис.1).В модели сущ-т прямые ^граничной прямой.(рис2).Расс-м в модели те аксиомы в кот-е не входит пон-е о рав-е отрез-в и улов. В данной модели вып-ся аксиома паралель-х:ч/з точку А,не лежащую на пр-й а,прох-т бесконеч-о много прямых, не имеющ-х с а общих точек.(рис1).Все прочие аксиомы о взаимном распол-и пр-х здесь выпол-ся. Так на (рис.3) постоим отрезок с данными концами.Затем возьмеи полуокр-ть,представ-ю прямую в модели, проведем пр-ю l,касающ-ся этой полуокр-ти и // гранич-й прям-й.спроект-м полуокр-ть из ее центра на пр-ю l.Получим взаимнооднознач-е, сохран-е порядок точек соответ-е м/у точ-и пр-й и полуокр-ти,т.е пр-й модели.Аксиома деления пл-ти также вып-ся. «Прямая»-полуокр-ть-делит пл-ть на 2 обл-ти-внутр-ю и внеш-ю.Это и будут полупл-ти в нашей модели.Из одной пл-ти нельзя перейти в др. по какой-либо дуге не пересекая раздел-ю их полуокр-ть.Опред-м рав-во отрез-в и улов. Это мы сделаем наложив наложение. Налож-е в модели назовем люб-ю композ-ю отражений.Равными наз-т фигуры совмещ-е наложением. Проективная модель геом-и Лоб-го.Пл-ть Лоб-го представ-ся внутр-ю круга,пр-е-хордами(с исключ-и концами,поскольку рассм-ся только внутр-ть круга).Преобр-я-отраж-я круга на себя,перевод-е хорды в хорды- приним-ся за наложения.,так что рав-и считают-ся фигуры внутри круга,кот-е отобр-ся одна на другую при таких преобр-х круга.преимущ-во этой модели в том, что пр-е изобр-ся наглядно-хордами-прямол-и отрез-ми.Модель названа проективной,т.к отобр-я,кот-е представ-т здесь наложения –это проект-е преобр-я соответ-о круга и шара.(рис4.) Пусть Е-не пустое мн-во.На мн-ве Е задана метрика r,если каж-й упоряд-й паре эл-в х, у принад-т Е постав-о в соответ-е неотриц-е вещ-е число r(х,у) т.о:1) r(х,у)=0«х=у 2) r(х,у)= r(у,х) для люб-х х и у.3) r(х,у)+ r(у,х)³ r(х,z).Ex/На непустом мн-е Е определим тривиальную метрику: r(х,у)={1,если х¹у; 0,если х=у
Векторы и операции над ними. Векторы в трёхмерном пространстве. Векторный и координатный методы решения задач. Отрезки АВ и СD называются эквиполлентными, если они одинаково направлены и имеют равные длины. Вектор – множество всех направленных отрезков, любые 2 из которых эквиполлентны. Операции над векторами: 1. возьмем произвольные векторы`а и`b. От какой-нибудь т.А отложим вектор АВ =`а, затем от т.В отложим вектор ВС=`b. Вектор АС=`с называется суммой векторов `а и`b и обозначается так: с = а + b. Для нахождения суммы 2 неколлинеарных векторов используют правило треугольника и параллелограмма. Для произвольных векторов а, b, с справедливы следующие равенства: 1) а + b = b + а. 2) (а + b) + c = a + (b + c). Для построения суммы нескольких векторов используется правило многоугольника. 2. Разностью векторов а и b называется такой вектор х, что b + x = a. 3. Произведением вектора а на число a называется вектор р, который удовлетворяет условиям: 1) |p|=|a||a|, где |a| - абсолютное значение числа a; 2) ра, если a³0 и р¯а, если a<0. Для произвольных чисел a, b и векторов а и b справедливы след.равенства: 1) 1×а=а и -1×а = -а. 2) a(bа) = (ab)а. 3) a(а + b)=aа + ab. 4) (a + b)а=aа + bа. 4. Скалярным произведением 2 векторов называется число, равное произведению их длин на косинус угла между ними. Для произвольного числа a и произвольных векторов а, b, с справедливы след.равенства: 1) ab = ba, 2) (aa)b = a(ab) и a(ab) = a(ab). 3) (a + b)c = ac + ab. 5. Смешанным произведением некомпланарных векторов а, b, с, взятых в данном порядке, называется объем параллелепипеда, построенного на этих векторах, снабженный знаком «-», если базис а, b, с правый, и знаком «+», если этот базис левый. Для произвольных векторов а, b, с, d и произвольного числа a имеют место след.равенства: 1) abc = bca = cab, 2) abc = -bac, abc = -cba, abc = -acb. 3) (aa)bc = a(abc), a(ab)c=a(abc), ab(ac)=a(abc). 4) (a+b)cd=acd+bcd, a(b+c)d=abd+acd, ab(c+d)= abc+abd. 6. Векторным произведением неколлинеарных векторов а и b, взятых в данном порядке, называется вектор р, длина которого численно равна площади параллелограмма, построенного на этих векторах; этот вектор ^векторам а и b и направлен так, что базис a, b, p имеет правую ориентацию. Для произвольных векторов a, b, c и произвольного числа a имеют место след.равенства: 1) [ab]=-[ba], 2) [aa,b]=a[ab], [a,(ab)]=a[ab], 3) [a+b,c]=[ac]+[bc], [a,b+c]=[ab]+[ac]. рассмотрим систему векторов а1, а2, …, аn и зададим n действительных чисел a1, a2, …, an. Вектор b=a1а1 + …+ anаn называется линейной комбинацией данных векторов. Система векторов называется линейно зависимой, если $числа a1, a2, …, an, среди которых хотя бы 1 отлично от 0, и такие, что a1а1 + …+ anаn = 0. Базисом векторного пространства называется такая система векторов, которая задана в определенном порядке и удовлетворяет условиям: 1) система линейно независима. 2) "вектор пространства является линейной комбинацией данной системы векторов. Пусть е1, е2, е3 – данный базис, а – произвольный вектор пространства. $единственные числа а1, а2, а3 такие, что: а=а1е1 + а2е2+а3е3. Говорят, что вектор а разложен по векторам базиса. Коэффициенты а1, а2, а3 называются координатами вектора а в этом базисе. Базис i, j, k называется ортонормированным, если его векторы удовлетворяют 2 условиям: 1) |i| = |j| = |k| = 1. 2) если ОЕ1 = i, OE2 = j, OE3 = k, то углы Е1ОЕ2, Е1ОЕ3 и Е2ОЕ3 прямые. Длина вектора а(а1, а2, а3) в ортонормированном базисе вычисляется по формуле: |a| =
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 151. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
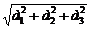 .
.