
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкойПри соотношении параметров контура из конденсатора, катушки и резистора p1,2 = -α ± jω, где α = R / (2L) – коэффициент затухания свободной составляющей; Поскольку
Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1) uCсв = A e-αt sin(ω0t + ψ), Для свободной составляющей тока iсв = C A e-αt (-α sin(ω0t + ψ) + ω0 cos(ω0t + ψ)). С учетом начальных условий при t = 0, uC = U0 , i = 0 из последних двух уравнений находим константы интегрирования: U0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cos ψ). и далее
Запишем переходные напряжения и ток: uC = UCm e-αt sin(ω0t + ψ); где
Зависимости переходных напряжения и тока uC, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т0, например:
Часто пользуются логарифмическим декрементом колебания:
В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона
Билет 20 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 525. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:
, где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные: – угловая частота собственных колебаний контура;
– угловая частота собственных колебаний контура; , то можно ввести обозначения
, то можно ввести обозначения ,
,  ,
,  .
. имеем
имеем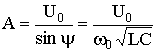 .
. ;
;  .
.
 .
. .
. , а частота незатухающих колебаний
, а частота незатухающих колебаний  .
.