
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дивергенция, циркуляция; ротор вектора, их свойства. Теорема Стокса. Условие потенциальности. Теорема Остроградского — Гаусса. Теорема Гаусса в дифференциальной формеСтр 1 из 2Следующая ⇒ [Дивергенция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток). Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учётом знака. Поэтому можно дать более короткое определение дивергенции: дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой в условиях конкретной задачи окрестности каждой внутренней точки области определения поля. Оператор дивергенции, применённый к полю
или
Определение дивергенции выглядит так:
где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся кнулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма ее внутренности). В обоих случаях подразумевается, что 
Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат, приведённые в следующем параграфе). Определение легко и прямо обобщается на любую размерность n пространства: при этом под объёмом понимается n-мерный объём, а под площадью поверхности (n-1)-мерная площадь (гипер)поверхности соответствующей размерности.
Дивергенция - одна из наиболее широко употребимых в физике операций. Представляет собой одно из достаточно немногих базовых понятий теоретической физики и является одним из базовых элементов физического языка. В стандартной формулировке классической теории поля дивергенция занимает центральное место (в альтернативных формулировках может не находиться в самом центре изложения, но всё равно остается важным техническим инструментом и важной идеей). В электродинамике дивергенция входит в качестве главной конструкции в два из четырёх уравнений Максвелла. Основное уравнение теории ньютоновской гравитации в полевом виде также содержит в качестве основной конструкции дивергенцию (напряженности гравитационного поля). В тензорных теориях гравитации (включая ОТО, и имея в виду в первую очередь её) основное полевое уравнение (в ОТО, но как правило - так или иначе - и в альтернативных современных теориях тоже) также включает в себя дивергенцию в некотором обобщении. То же можно сказать о классической (т.е. неквантовой) теории практически любого из фундаментальных полей, как экспериментально известных, так и гипотетических. Помимо этого, как видно из приведённых выше примеров, дивергенция применима и в чисто геометрическом плане, а также - особенно часто - к различным материальным потокам (дивергенция скорости течения жидкости или газа, дивергенция плотности электрического тока и т.п.). Свойства Следующие свойства могут быть получены из обычных правил дифференцирования. · Линейность: для любых векторных полей F и G и для всех вещественных чисел a и b
· Если φ — скалярное поле, а F — векторное, тогда:
· Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:
· Дивергенция от градиента есть лапласиан:
· Дивергенция от ротора:
.Циркуляция. Пусть Λ пространственная кусочно-гладкая линия и пусть a(M) – непрерывное векторное поле, заданное в Λ⊂Т⊂R3. Обозначим проекции вектора a(M) на координатные оси: P(M), Q(M), R(M). Определение. Криволинейный интеграл вида ∫ Λ P(x, y,z)dx + Q(x, y,z)dy + R(x, y,z)dz , взятый по направленной линии Λ называется линейным интегралом от вектора а вдоль линии Λ. Определение. Циркуляцией векторного поля a=(P, Q, R) по замкнутой линии Λ в области T⊂R3: называется линейный интеграл по этой замкнутой линии Λ, Ц= ∫ Λ adr , где dr=(dx, dy, dz) – вектор-дифференциал. Таким образом, ∫ ∫ Λ Λ adr = пр adl τ , где τ=(cosα, cosβ, cosγ) – единичный касательный вектор, dl – элемент дуги Λ, прτa – проекция вектора а на касательную τ.
Теорема Гаусса: поток электрической индукции через любую замкнутую поверхность равен алгебраической сумме всех зарядов, находящихся внутри поверхности: Из формулы видно, что размерность электрического потока такая же, как и электрического заряда. Поэтому единицей потока электрической индукции служит кулон (Кл). Примечание: если поле неоднородно и поверхность, через которую определяют поток, не является плоскостью, то эту поверхность можно разбить на бесконечно малые элементы ds и каждый элемент считать плоским, а поле возле него однородным. Поэтому для любого электрического поля поток вектора электрической индукции через элемент поверхности есть: dФ = Это одно из фундаментальных уравнений Максвелла для электромагнитного поля, записанное в интегральной форме. Оно показывает, что источником постоянного во времени электрического поля являются неподвижные электрические заряды. |
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 437. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
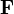 , обозначают как
, обозначают как
 .
.
 .
.
 или
или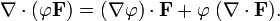
 или
или





 компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,
компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,
 где через
где через
 обозначена дивергенция векторного поля
обозначена дивергенция векторного поля  (она обозначается также символом
(она обозначается также символом  ). Символ
). Символ  указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме:
указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме:
 В частном случае, полагая
В частном случае, полагая  , получаем формулу для вычисления объема тела G:
, получаем формулу для вычисления объема тела G:

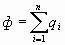 .
. . В результате интегрирования полный поток через замкнутую поверхность S в любом неоднородном электрическом поле равен:
. В результате интегрирования полный поток через замкнутую поверхность S в любом неоднородном электрическом поле равен:  , где q – алгебраическая сумма всех зарядов, окружённых замкнутой поверхностью S. Выразим последнее уравнение через напряжённость электрического поля (для вакуума):
, где q – алгебраическая сумма всех зарядов, окружённых замкнутой поверхностью S. Выразим последнее уравнение через напряжённость электрического поля (для вакуума):  .
.