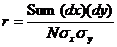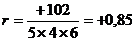Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Корреляция как произведение моментов
Чаще всего коэффициент корреляции определяется методом произведения моментов; получаемый в результате индекс обычно обозначается маленькой буквой r. Вычисленный через произведение моментов коэффициент r варьируется между полной положительной корреляцией (r = +1,00) и полной отрицательной корреляцией (r = -1,00). Отсутствие всякой связи дает r = 0,00. Корреляция вычисляется через произведение моментов по формуле:
Здесь одну из парных мер называют x-показателем, а другую y-показателем, dx и dy — это отклонения каждого показателя от среднего; N — количество парных величин, а σx и σy — стандартные отклонения x-показателей и y-показателей. Для определения коэффициента корреляции надо определить сумму произведений (dx) x (dy). Эту сумму вместе с вычисленными стандартными отклонениями для х-показателей и y-показателей можно затем подставить в формулу. Пример вычисления корреляции через произведение моментов.Предположим, мы собрали данные, показанные в табл. П6. Для каждого испытуемого получено два показателя; первый — оценка на вступительных экзаменах (ее мы произвольно назовем x-показателем), а второй — оценки за первый курс (y-показатель).
Таблица П6. Вычисление корреляции через произведение моментов
σx = 4, σy = 6
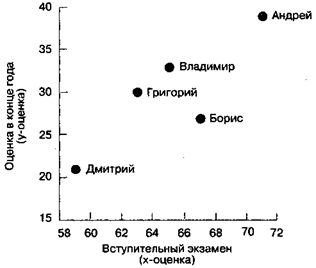
На рис. П6 показан точечный график этих данных. Каждая точка отражает x-показатель и y-показатель данного человека; например, верхняя точка справа означает Андрея. Глядя на эти данные, легко обнаружить, что между х- и у-показателями существует некоторая положительная корреляция. Андрей получил наивысшую оценку на вступительном экзамене и также получил наивысшую отметку за 1-й курс; Дмитрий получил и там, и там самую низкую отметку. В показателях других студентов есть немного нерегулярности, так что мы знаем, что корреляция не полная; следовательно, r меньше 1,00. 
Рис. П6. Точечная диаграмма.Каждая точка отражает х- и у-показатели определенного учащегося.
Мы подсчитаем корреляцию, чтобы проиллюстрировать этот метод, хотя на практике ни один исследователь не станет считать корреляцию для столь малого количества показателей. Подробности приведены в табл. П6. Согласно процедуре, приведенной в табл. П3, мы вычисляем стандартное отклонение x-показателей, а затем стандартное отклонение y-показателей. Затем мы вычисляем произведение (dx) x (dy) для каждого человека и для 5 случаев в общем. Подставляя полученные числа в уравнение, получаем r = +0.85.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 424. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |