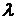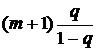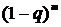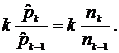Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моделирование частот наступления убытковВ соответствии с исследованиями наиболее распространенными распределениями, применяемыми для моделирования частот наступления событий операционного риска, являются отрицательное биномиальное и смеси распределений Пуассона. В рамках реализации модели LDA учтены рекомендованные Базель II упрощения касательно наличия идеальной корреляции между убытками. Калибровка распределений. Класс (а,Ь,0) 1. Распределение Пуассона: 2. Отрицательное биномиальное распределение. Благодаря наличию второго параметра, форма отрицательного биномиального распределения является более гибкой, что позволяет проще калибровать ее к текущему профилю операционных потерь. Оценки параметров распределений на основании метода максимального правдоподобия для распределений Пуассона и отрицательного биномиального имеют следующий вид:
Класс (a,b,0) Определение Дискретное распределение
К классу Таблица 1 Распределения принадлежащие классу
Рекурсивную формулу 2.8 удобно использовать для подбора наиболее подходящего распределения частоты наступления событий, на основе исторических данных:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 352. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
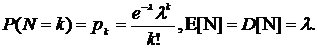 Сумма
Сумма  независимых Пуассоновых случайных величин (ссоответствующими параметрами распределения
независимых Пуассоновых случайных величин (ссоответствующими параметрами распределения  также распределена по закону Пуассона с параметром
также распределена по закону Пуассона с параметром 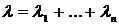 .
.
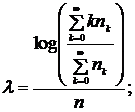
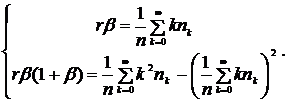
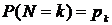 принадлежит классу
принадлежит классу  , если существуют такие
, если существуют такие 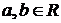 :
: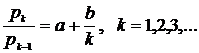 (2.8)
(2.8)