
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ЕЕ ОСНОВНЫЕ СВОЙСТВА Сведения из теории Случайная величина – переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее не известно). Случайные величины обозначают большими латинскими буквами Х, Y,…, а принимаемые ими значения – малыми буквами Случайные величины бывают дискретными и непрерывными. Дискретная (прерывная) случайная величина – это величина, множество значений которой конечное, или бесконечное, но счетное, т.е. если его элементы можно перенумеровать натуральными числами (например, число родившихся детей в течение суток в г. Сургуте). Непрерывная случайная величина – это величина бесконечное несчетное множество значений, которой есть некоторый интервал (конечный или бесконечный) числовой оси (например, расход электроэнергии на предприятии в месяц). Используя теоретика-множественную трактовку, можно дать боле строгое определение: случайной величиной Х называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т.е. Наиболее полным, исчерпывающим описанием случайной величины является её закон распределения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.  Закон распределения дискретной случайной величины удобно задавать с помощью следующей таблицы:
где Такая таблица называется рядом распределения дискретной случайной величины. Сумма вероятностей равна единице (эта единица как-то распределена между значениями случайной величины, отсюда и термин «распределение»). Графически ряд распределения изображают в виде многоугольника (или полигона) распределения (рис. 5).
Рис. 5
Числовые характеристики Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда выгоднее пользоваться числами, которые описывают случайную величину. Такие числа называются числовыми характеристиками случайной величины. Математическое ожидание Математическим ожиданием, или средним значением, M(X) дискретной случайной величины 1. M(X) заключено между наименьшим и наибольшим значениями случайной величины. 2. M(X) рассматривают как характеристику положения случайной величины, её центр распределения. Свойства математического ожидания 1. M(C) = C, где C – const. 2. 3. 4. 5. 6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0. Теорема.M(X) числа появлений события A в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании, т.е. M(X) = np. Дисперсия Математическое ожидание не характеризует полностью случайную величину. То есть, нельзя судить о том, какие возможные значения принимает случайная величина, зная лишь её M(X). Дисперсия позволяет оценить как рассеяны возможные значения случайной величины от среднего. D(X) случайной величины X называется математическое ожидание квадрата её отклонения от математического ожидания
или
D(X) есть величина неотрицательная. Теорема.Математическое ожидание отклонения равно 0, Свойства дисперсии 1. D(C) = 0, где C – const. 2. 3. Теорема.Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании, т.е. D(X) = npq.
Среднее квадратическое отклонение Для оценки рассеяния возможных значений случайной величины вокруг её среднего значения кроме дисперсии служит и среднее квадратическое отклонение. Средним квадратическим отклонением называется корень квадратный из дисперсии Теорема.Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин, т.е.
Начальные и центральные теоретические моменты Начальным моментом k-го порядка случайной величины
Пользуясь начальными моментами, формулу для вычисления дисперсии можно переписать так: Центральным моментом порядка k случайной величины X называется математическое ожидание k-ой степени отклонения
В частности, Соотношения, связывающие начальные и центральные моменты, т.е.
Моменты более высоких порядков применяются редко. |
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  …,
…,  ,
,  …
… , где
, где  – элементарный исход.
– элементарный исход.
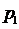

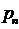
 .
.
 называется сумма произведений всех ее значений на соответствующие им вероятности
называется сумма произведений всех ее значений на соответствующие им вероятности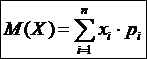 . (34 )
. (34 ) 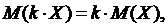 где k – постоянный множитель.
где k – постоянный множитель.
 где X, Y – независимые случайные величины.
где X, Y – независимые случайные величины.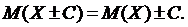

 (35)
(35)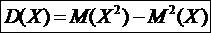 . (36)
. (36)
 где k – постоянный множитель.
где k – постоянный множитель.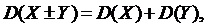 где X, Y – независимые случайные величины.
где X, Y – независимые случайные величины. . (37)
. (37)

 . (38)
. (38)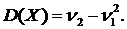
 . (39)
. (39)
 ,
, ,
, .
.